题目内容
若等比数列{an}的前n项和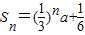 ,则a= .
,则a= .
【答案】分析:由题意解出a1,和n≥2时的通项公式,由数列{an}为等比数列可知,把n=1代入n≥2时式子求得的值应等于n=1时求解的a1,由此可解a的值.
解答:解:当n=1时,a1=S1=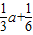 ,
,
当n≥2时,an=Sn-Sn-1
=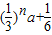 -
-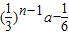 =-2
=-2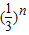 a,
a,
由数列{an}为等比数列可知: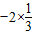 a=
a=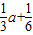 ,
,
解得a=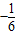 ,
,
故答案为: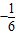
点评:本题为等比数列的通项公式和求和公式的关系的应用,属基础题.
解答:解:当n=1时,a1=S1=
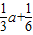 ,
,当n≥2时,an=Sn-Sn-1
=
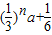 -
-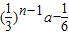 =-2
=-2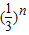 a,
a,由数列{an}为等比数列可知:
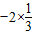 a=
a=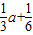 ,
,解得a=
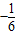 ,
,故答案为:
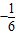
点评:本题为等比数列的通项公式和求和公式的关系的应用,属基础题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目