题目内容
已知a=(cosx+sinx,sinx),b=(cosx-sinx,2cosx),设f(x)=a·b。
(1)求函数f(x)的单调增区间;
(2)三角形ABC的三个角A,B,C所对边分别是a,b,c,且满足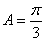 ,f(B)=1,
,f(B)=1,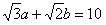 ,求边c。
,求边c。
(1)求函数f(x)的单调增区间;
(2)三角形ABC的三个角A,B,C所对边分别是a,b,c,且满足
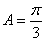 ,f(B)=1,
,f(B)=1,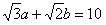 ,求边c。
,求边c。解:(1)∵f(x)=a·b=(cosx+sinx)·(cosx-sinx)+sinx·2cosx
=cos2x-sin2x+2sinxcosx=cos2x+sin2x
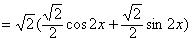
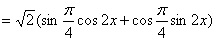
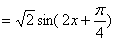
由f(x)递增得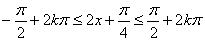
即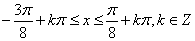
∴f(x)的递增区间是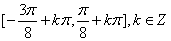 。
。
(2)由f(B)=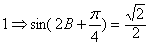
及0<B<π得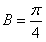
设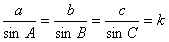
则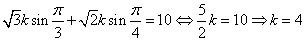
所以c=ksinC=4sin(A+B)
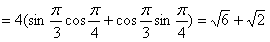 。
。
=cos2x-sin2x+2sinxcosx=cos2x+sin2x
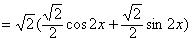
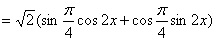
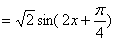
由f(x)递增得
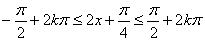
即
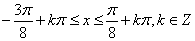
∴f(x)的递增区间是
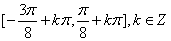 。
。(2)由f(B)=
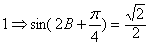
及0<B<π得
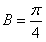
设
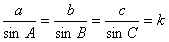
则
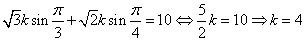
所以c=ksinC=4sin(A+B)
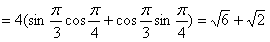 。
。
练习册系列答案
相关题目