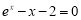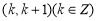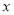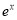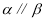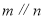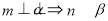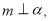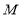题目内容
已知函数
.
(1)求函数
的最小正周期和图像的对称轴方程；
(2)求函数
在区间
上的值域.
（1）
，
；（2）
【解析】
试题分析：（1）先利用两角和与差的三角函数将式子展开合并，再利用二倍角公式、辅助角公式化简得到
，再结合正弦函数的性质，由
、
可得函数
的最小正周期与对称轴的方程；（2）将
当成整体，由
，利用正弦函数的单调性可得
，即
的值域.
试题解析：（1）
所以函数
的周期
由
，得
所以函数
图像的对称轴方程为
6分
（2）因为
，所以
因为
在区间
上单调递增，在区间
上单调递减
所以当
时，
取最大值1
又因为
，当
时，
取最小值
所以函数
在区间
上的值域为
10分.
考点：1.三角函数的图像与性质；2.三角恒等变换.
练习册系列答案
相关题目
