Question

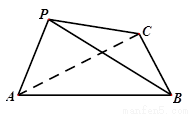
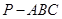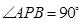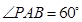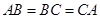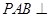(本小题满分12分) 如图，在三棱锥中，，，，平面平面。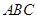

（Ⅰ）求直线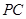与平面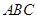所成角的大小；

（Ⅱ）求二面角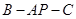的大小。

 

Answer 1

【答案】

 

【解析】（1）连接OC。由已知，所成的角

设AB的中点为D，连接PD、CD.

因为AB=BC=CA,所以CDAB.

因为等边三角形，

不妨设PA=2，则OD=1，OP=,AB=4.

所以CD=2，OC=.

在Rttan.

故直线PC与平面ABC所成的角的大小为arctan…………………6分

（2）过D作DE于E，连接CE.       

     由已知可得，CD平面PAB.

根据三垂线定理可知，CE⊥PA，

所以，.

由（1）知，DE=

在Rt△CDE中，tan

故……………………………12分

[点评]本小题主要考查线面关系、直线与平面所成的角、二面角等基础知识，考查思维能力、空间想象能力，并考查应用向量知识解决数学问题的能力.