题目内容
20.一场晚会有4个唱歌节目和2个舞蹈节目,要求排出一个节目单.(1)第一个节目是舞蹈.有多少种排法?
(2)2个舞蹈节目要排在一起,有多少种排法?
(3)2个舞蹈节目彼此要隔开,有多少种排法?
分析 (1)先从2个舞蹈节目选一个排在第一个节目,其余的节目全排,问题得以解决.
(2)要把2个舞蹈节目要排在一起,则可以采用捆绑法,把三个舞蹈节目看做一个元素和另外4个元素进行全排列.
(3)2个舞蹈节目彼此要隔开,可以用插空法来解,即先把4个唱歌节目排列,形成5个位置,选2个把舞蹈节目排列.
解答 解(1)先从2个舞蹈节目选一个排在第一个节目,其余的节目全排,故有A21A55=240种,
(2)2个舞蹈节目要排在一起,把2个舞蹈节目看做一个元素和另外4个元素进行全排列,2个舞蹈节目本身也有一个排列有A55A22=240种,
(3)2个舞蹈节目彼此要隔开,可以用插空法来解,先把4个唱歌节目排列,形成5个位置,选2个把舞蹈节目排列,有A44A52=480种.
点评 本题是一个排列组合典型,实际上所有的排列都可以看作是先取组合,再做全排列;同样,组合如补充一个阶段(排序)可转化为排列问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.圆x2+y2=1与圆x2+y2+2x+2y+1=0的交点坐标为( )
| A. | (1,0)和(0,1) | B. | (1,0)和(0,-1) | C. | (-1,0)和(0,-1) | D. | (-1,0)和(0,1) |
15.若变量x,y满足$\left\{\begin{array}{l}{2x+y-5≥0}\\{x-y+5≥0}\\{2x-y-5≤0}\end{array}\right.$ 则x2+y2的最小值为( )
| A. | $\frac{25}{4}$ | B. | $\frac{5}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
1.已知复数z=1+i(i是虚数单位),则$\frac{2}{z}$-z2的共轭复数是( )
| A. | -1+3i | B. | 1+3i | C. | 1-3i | D. | -1-3i |
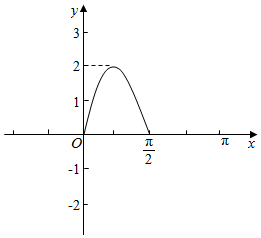 已知函数f(x)=2sinωx(ω>0)的部分图象如图所示.
已知函数f(x)=2sinωx(ω>0)的部分图象如图所示.