题目内容
给出定义:若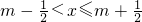 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:
①函数y=f(x)的定义域是R,值域是[0, ];
];
②函数y=f(x)的图象关于直线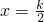 (k∈Z)对称;
(k∈Z)对称;
③函数y=f(x)是周期函数,最小正周期是1;
则其中真命题是________.
①②③
分析:定义域显然为R,然后根据题设x≤m+ ,{x}=m,则f(x)=x-{x}≤
,{x}=m,则f(x)=x-{x}≤ ;
;
f(k-x)=|(k-x)-{k-x}|=|(-x)-{-x}|=f(-x),所以关于x=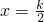 (k∈Z)对称;
(k∈Z)对称;
f(x+1)=|(x+1)-{x+1}|=|x-{x}|=f(x),所以周期为1.
解答:①定义域显然为R,然后根据题设x≤m+ ,{x}=m,
,{x}=m,
则f(x)=x-{x}≤ ,故①成立;
,故①成立;
②f(k-x)=|(k-x)-{k-x}|=|(-x)-{-x}|=f(-x),
所以关于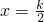 (k∈Z)对称,故②成立;
(k∈Z)对称,故②成立;
③f(x+1)=|(x+1)-{x+1}|=|x-{x}|=f(x),
所以周期为1,故③成立.
故答案为:①②③.
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答,注意函数的定义域、值域、对称性和周期性的求法.
分析:定义域显然为R,然后根据题设x≤m+
 ,{x}=m,则f(x)=x-{x}≤
,{x}=m,则f(x)=x-{x}≤ ;
;f(k-x)=|(k-x)-{k-x}|=|(-x)-{-x}|=f(-x),所以关于x=
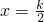 (k∈Z)对称;
(k∈Z)对称;f(x+1)=|(x+1)-{x+1}|=|x-{x}|=f(x),所以周期为1.
解答:①定义域显然为R,然后根据题设x≤m+
 ,{x}=m,
,{x}=m,则f(x)=x-{x}≤
 ,故①成立;
,故①成立;②f(k-x)=|(k-x)-{k-x}|=|(-x)-{-x}|=f(-x),
所以关于
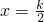 (k∈Z)对称,故②成立;
(k∈Z)对称,故②成立;③f(x+1)=|(x+1)-{x+1}|=|x-{x}|=f(x),
所以周期为1,故③成立.
故答案为:①②③.
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答,注意函数的定义域、值域、对称性和周期性的求法.

练习册系列答案
相关题目
 (其中m为整数),则m叫做离实数x最近的整数,记作{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:
(其中m为整数),则m叫做离实数x最近的整数,记作{x}=m.在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题: ;
; (k∈Z)对称;
(k∈Z)对称; 上是增函数.
上是增函数. (其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题:
(其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题: ; ②函数f(x)是R上的增函数;
; ②函数f(x)是R上的增函数; (其中m为整数),则m叫做离实数x最近的整数,记作
(其中m为整数),则m叫做离实数x最近的整数,记作 ,在此基础上给出下列关于函数
,在此基础上给出下列关于函数 的四个命题:①函数
的四个命题:①函数 的定义域为
的定义域为 ,值域为
,值域为 ;②函数
;②函数 上是增函数;③函数
上是增函数;③函数 ;④函数
;④函数
 对称.其中正确命题的序号是 .
对称.其中正确命题的序号是 . (其中m为整数),则m叫做离实数x最近的整数,记作{x},即
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即 .在此基础上给出下列关于函数
.在此基础上给出下列关于函数 的四个命题:
的四个命题: 的定义域是R,值域是
的定义域是R,值域是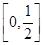 ;
; 对称;
对称; 上是增函数.
上是增函数. (其中m为整数),则m叫做离实数x最近的整数,记作{x},即
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即 ,在此基础上给出下列关于函数
,在此基础上给出下列关于函数 的四个命题:
的四个命题: 的定义域是R,值域是
的定义域是R,值域是 ;
; 的图像的对称中心;
的图像的对称中心; 上是增函数;
上是增函数;