题目内容
设函数f(x)=x2,g(x)=mlnx(m>0),已知f(x)与g(x)有且仅有一个公共点.
(1)求m的值;
(2)对于函数h(x)=ax+b(a,b∈R),若存在a,b,使得关于x的不等式g(x)≤h(x)≤f(x)+1对于g(x)定义域上的任意实数x恒成立,求a的最小值以及对应的h(x)的解析式.
解:(1)令f(x)=g(x),即x2=mlnx(x>0),
可得 ,设
,设 ,
,
则 ,
,
令p'(x)=0,得 .
.
当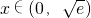 时,p'(x)>0,p(x)递增;
时,p'(x)>0,p(x)递增;
当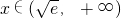 时,p'(x)<0,p(x)递减.
时,p'(x)<0,p(x)递减.
考虑到x∈(0,1]时,
 时,
时, ;
; 时,
时, .
.
考虑到m>0,故 ,因此m=2e.…(4分)
,因此m=2e.…(4分)
(2)由(1)知,g(x)=2elnx.
g(x)≤h(x)≤f(x)+1,可知a>0. …(6分)
(ⅰ)由h(x)≤f(x)+1对x∈(0,+∞)恒成立,
即x2-ax-b+1≥0对x∈(0,+∞)恒成立,
所以△=(-a)2-4(-b+1)≤0,
解得 ①.…(8分)
①.…(8分)
(ⅱ)由g(x)≤h(x)对x∈(0,+∞)恒成立,
即2elnx-ax-b≤0对x∈(0,+∞)恒成立,
设G(x)=2elnx-ax-b,x∈(0,+∞),
则 ,
,
令G'(x)=0,得 .
.
当 时,G'(x)>0,G(x)递增;
时,G'(x)>0,G(x)递增;
当 时,G'(x)<0,G(x)递减.
时,G'(x)<0,G(x)递减.
故 ,
,
则须 ,即得
,即得 ②.
②.
由①②得 ③. …(10分)
③. …(10分)
存在a,b,使得③成立的充要条件是:
不等式 ④有解.…(12分)
④有解.…(12分)
不等式④可化为 ,
,
即 ,
,
令 ,则有-t2+2elnt+1≥0,
,则有-t2+2elnt+1≥0,
设φ(t)=-t2+2elnt+1,
则 ,
,
可知φ(t)在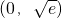 上递增,
上递增,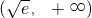 上递减.
上递减.
又φ(1)=0, ,
,
φ(e)=-e2+2elne+1=-e2+2e+1<0,
所以φ(t)=-t2+2elnt+1在区间 内存在一个零点t0,
内存在一个零点t0,
故不等式-t2+2elnt+1≥0的解为1≤t≤t0,
即 ,得2≤a≤2t0.
,得2≤a≤2t0.
因此a的最小值为2,代入③得0≤b≤0,故b=0,
对应的h(x)的解析式为h(x)=2x. …(16分)
分析:(1)令x2=mlnx(x>0),得 ,设
,设 ,令p'(x)=0,得
,令p'(x)=0,得 .再结合函数的单调性,能求出m的值.
.再结合函数的单调性,能求出m的值.
(2)由g(x)=2elnx.g(x)≤h(x)≤f(x)+1,可知a>0.(ⅰ)由x2-ax-b+1≥0对x∈(0,+∞)恒成立,知△=(-a)2-4(-b+1)≤0,解得 .(ⅱ)由2elnx-ax-b≤0对x∈(0,+∞)恒成立,设G(x)=2elnx-ax-b,x∈(0,+∞),利用导数解得得
.(ⅱ)由2elnx-ax-b≤0对x∈(0,+∞)恒成立,设G(x)=2elnx-ax-b,x∈(0,+∞),利用导数解得得 .由此能求出对应的h(x)的解析式.
.由此能求出对应的h(x)的解析式.
点评:本题考查利用导数求函数在闭区间上的最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.
可得
 ,设
,设 ,
,则
 ,
,令p'(x)=0,得
 .
.当
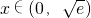 时,p'(x)>0,p(x)递增;
时,p'(x)>0,p(x)递增;当
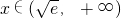 时,p'(x)<0,p(x)递减.
时,p'(x)<0,p(x)递减.考虑到x∈(0,1]时,
 时,
时, ;
; 时,
时, .
.考虑到m>0,故
 ,因此m=2e.…(4分)
,因此m=2e.…(4分)(2)由(1)知,g(x)=2elnx.
g(x)≤h(x)≤f(x)+1,可知a>0. …(6分)
(ⅰ)由h(x)≤f(x)+1对x∈(0,+∞)恒成立,
即x2-ax-b+1≥0对x∈(0,+∞)恒成立,
所以△=(-a)2-4(-b+1)≤0,
解得
 ①.…(8分)
①.…(8分)(ⅱ)由g(x)≤h(x)对x∈(0,+∞)恒成立,
即2elnx-ax-b≤0对x∈(0,+∞)恒成立,
设G(x)=2elnx-ax-b,x∈(0,+∞),
则
 ,
,令G'(x)=0,得
 .
.当
 时,G'(x)>0,G(x)递增;
时,G'(x)>0,G(x)递增;当
 时,G'(x)<0,G(x)递减.
时,G'(x)<0,G(x)递减.故
 ,
,则须
 ,即得
,即得 ②.
②.由①②得
 ③. …(10分)
③. …(10分)存在a,b,使得③成立的充要条件是:
不等式
 ④有解.…(12分)
④有解.…(12分)不等式④可化为
 ,
,即
 ,
,令
 ,则有-t2+2elnt+1≥0,
,则有-t2+2elnt+1≥0,设φ(t)=-t2+2elnt+1,
则
 ,
,可知φ(t)在
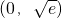 上递增,
上递增,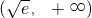 上递减.
上递减.又φ(1)=0,
 ,
,φ(e)=-e2+2elne+1=-e2+2e+1<0,
所以φ(t)=-t2+2elnt+1在区间
 内存在一个零点t0,
内存在一个零点t0,故不等式-t2+2elnt+1≥0的解为1≤t≤t0,
即
 ,得2≤a≤2t0.
,得2≤a≤2t0.因此a的最小值为2,代入③得0≤b≤0,故b=0,
对应的h(x)的解析式为h(x)=2x. …(16分)
分析:(1)令x2=mlnx(x>0),得
 ,设
,设 ,令p'(x)=0,得
,令p'(x)=0,得 .再结合函数的单调性,能求出m的值.
.再结合函数的单调性,能求出m的值.(2)由g(x)=2elnx.g(x)≤h(x)≤f(x)+1,可知a>0.(ⅰ)由x2-ax-b+1≥0对x∈(0,+∞)恒成立,知△=(-a)2-4(-b+1)≤0,解得
 .(ⅱ)由2elnx-ax-b≤0对x∈(0,+∞)恒成立,设G(x)=2elnx-ax-b,x∈(0,+∞),利用导数解得得
.(ⅱ)由2elnx-ax-b≤0对x∈(0,+∞)恒成立,设G(x)=2elnx-ax-b,x∈(0,+∞),利用导数解得得 .由此能求出对应的h(x)的解析式.
.由此能求出对应的h(x)的解析式.点评:本题考查利用导数求函数在闭区间上的最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目