题目内容
设an是公差不为零的等差数列,Sn为其前n项和,满足a22+a32=a42+a52,S7=7
(1)求数列an的通项公式及前n项和Sn;
(2)试求所有的正整数m,使得 为数列an中的项.
为数列an中的项.
(1)求数列an的通项公式及前n项和Sn;
(2)试求所有的正整数m,使得
 为数列an中的项.
为数列an中的项.解:(1)由题意可得
联立可得a1=﹣5,d=2
∴an=﹣5+(n﹣1)×2=2n﹣7,

(2)由(1)知 =
=
若使为数列an中的项则 必需为整数,且m为正整数m=2,m=1;
必需为整数,且m为正整数m=2,m=1;
m=1时不满足题意,(a1=﹣5是最小值)故舍去.
所以m=2.

联立可得a1=﹣5,d=2
∴an=﹣5+(n﹣1)×2=2n﹣7,

(2)由(1)知
 =
=
若使为数列an中的项则
 必需为整数,且m为正整数m=2,m=1;
必需为整数,且m为正整数m=2,m=1;m=1时不满足题意,(a1=﹣5是最小值)故舍去.
所以m=2.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
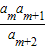 为数列an中的项.
为数列an中的项.