Question

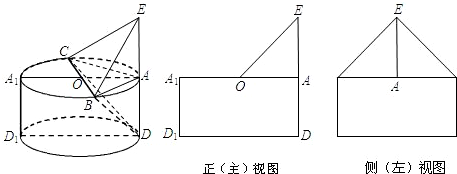
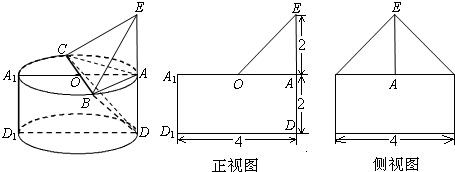
一个几何体是由圆柱ADD₁A₁和三棱锥E-ABC组合而成，点A、B、C在圆O的圆周上，其正（主）视图、侧（左）视图的面积分别为10和12，如图2所示，其中EA⊥平面ABC，AB⊥AC，AB=AC，AE=2．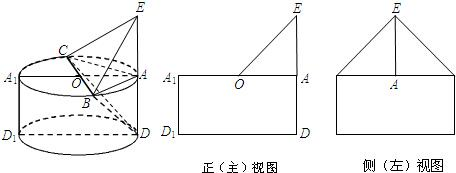

（1）求证：AC⊥BD；
（2）求三棱锥E-BCD的体积．

Answer 1

分析：（1）由已知中EA⊥平面ABC，AB⊥AC，结合线面垂直的定义及线面垂直的判定定理，我们易求出AC⊥平面EBD，进而得到答案．
（2）要求三棱锥E-BCD的体积，我们有两种办法，
方法一是利用转化思想，将三棱锥E-BCD的体积转化为三棱锥C-EBD的体积，求出棱锥的高和底面面积后，代入棱锥体积公式，进行求解；
方法二是根据V_E-BCD=V_E-ABC+V_D-ABC，将棱锥的体积两个棱次的体积之差，求出两个辅助棱锥的体积后，得到结论．

解答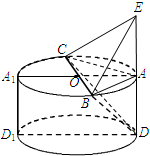：（1）证明：因为EA⊥平面ABC，AC?平面ABC，所以EA⊥AC，即ED⊥AC．
又因为AC⊥AB，AB∩ED=A，所以AC⊥平面EBD．
因为BD?平面EBD，所以AC⊥BD．（4分）
（2）解：因为点A、B、C在圆O的圆周上，且AB⊥AC，所以BC为圆O的直径．
设圆O的半径为r，圆柱高为h，根据正（主）视图、侧（左）视图的面积可得，

2rh+ 1 2 r×2=10 2rh+ 1 2 ×2r×2=12.

（6分）
解得

r=2 h=2.

所以BC=4，AB=AC=2

2

．
以下给出求三棱锥E-BCD体积的两种方法：
方法1：由（1）知，AC⊥平面EBD，
所以VE-BCD=VC-EBD=

1

3

S△EBD×CA．（10分）
因为EA⊥平面ABC，AB?平面ABC，
所以EA⊥AB，即ED⊥AB．
其中ED=EA+DA=2+2=4，因为AB⊥AC，AB=AC=2

2

，
所以S△EBD=

1

2

×ED×AB=

1

2

×4×2

2

=4

2

．（13分）
所以VE-BCD=

1

3

×4

2

×2

2

=

16

3

．（14分）
方法2：因为EA⊥平面ABC，
所以VE-BCD=VE-ABC+VD-ABC=

1

3

S△ABC×EA+

1

3

S△ABC×DA=

1

3

S△ABC×ED．（10分）
其中ED=EA+DA=2+2=4，因为AB⊥AC，AB=AC=2

2

，
所以S△ABC=

1

2

×AC×AB=

1

2

×2

2

×2

2

=4．（13分）
所以VE-BCD=

1

3

×4×4=

16

3

．（14分）

点评：本题考查的知识点是棱锥的体积公式，简单空间图形的三视图，直线与平面垂直的性质，其中根据已知中三视图的体积，判断出几何体中相关几何量的大小，结合已知中其中量，进而判断出线面关系是解答本题的关键．