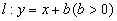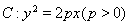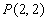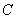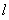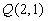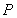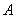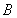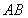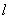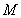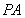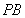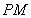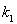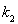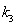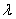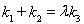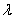题目内容
已知
两点在抛物线
上，点
满足
（I）求证：
；
（Ⅱ）设抛物线
过两点的切线交于点
（1）求证：点N在一定直线上；
（2）设
，求直线
在
轴上截距的取值范围。
解析:
解：设A
，与
联立得
（Ⅰ）
=
（Ⅱ）（1）过点A的切线：
①
过点B的切线：
②
联立①②得点N（
所以点N在定直线
上
（2）
联立
可得
直线MN：
在
轴的截距为
直线MN在轴上截距的取值范围是
练习册系列答案
相关题目
在抛物线
上，
点到抛物线
的焦点F的距离为2，
与抛物线交于
两点.
为直径的圆与
轴相切，求该圆的方程；
与
轴负半轴相交，求
面积的最大值.
在抛物线
上，
点到抛物线
的焦点F的距离为2，
与抛物线交于
两点.
为直径的圆与
轴相切，求该圆的方程；
与
轴负半轴相交，求
面积的最大值.
在抛物线
上，
点到抛物线
的焦点F的距离为2，
与抛物线交于
两点.
为直径的圆与
轴相切，求该圆的方程；
与
轴负半轴相交，求
面积的最大值.
