题目内容

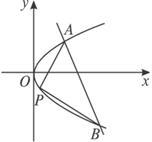
已知直线x+2y-4=0与抛物线y2=4x相交于A、B两点，O是坐标原点，试在抛物线的弧弧AOB上求一点P，使△PAB面积最大.

解：|AB|为定值，△PAB面积最大，只要点P到AB的距离最大，只要点P是抛物线的平行于AB的切线的切点，设P（x,y）.由图可知，点P在x轴下方的图象上,

∴y=-2.∴y′=-.

∵kAB=-,∴-=-.

∴x=4,代入y2=4x(y＜0)得y=-4.∴P(4,-4).

练习册系列答案
相关题目
精英家教网选做题（考生只能从A、B、C题中选作一题）
A、已知直线x+2y-4=0与
x=2-3cosθ
y=1+3sinθ
（θ为参数）相交于A、B两点，则|AB|=
 
．
B、若关于x的方程x2+4x+|a-1|+|a+1|=0有实根，则实数a的取值范围为
 
．
C、如图，⊙O的直径AB=6cm，P是延长线上的一点，过点P作⊙O的切线，切点为C，连接AC，若∠CAP=30°，
则PC=
 
cm．
已知直线x-2y+4=0经过椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左顶点A和上顶点D，椭圆C的右顶点为B，点P是椭圆C上位于x轴上方的动点，直线AP，BP与直线l：x=5分别交于M，N两点．
（1）求椭圆C的方程；
（2）求线段MN的长度的最小值；
（3）当线段MN的长度最小时，Q点在椭圆上运动，记△BPQ的面积为S，当S在（0，+∞）上变化时，讨论S的大小与Q点的个数之间的关系．
已知直线x+2y-4=0与
x=2-3cosθ
y=1+3sinθ
（θ为参数）相交于A、B两点，则|AB|=
6
6
．
选做题：（考生注意：请在下列三题中任选一题作答，如果多做，则按所做第一题评分）
A．（不等式选做题）不等式
x+5
(x-1)2
≥2的解集是
[-
1
2
，1）∪（1，3]
[-
1
2
，1）∪（1，3]
．
B．（几何证明选做题） 如图，⊙O的直径AB=6cm，P是延长线上的一点，过点P作⊙O的切线，切点为C，连接AC，若∠CAP=30°，则PC=
3
3
3
3
．
C．（坐标系与参数方程选做题）已知直线x+2y-4=0与
x=2-3cosθ
y=1+3sinθ
（θ为参数）相交于A、B两点，则|AB|=
6
6
．
已知直线x+2y-4=0,则直线的斜率为__________,倾斜角为__________,在x轴、y轴上的截距分别为__________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网