题目内容
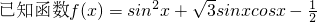
(1)求函数f(x)的最小正周期.
(2)求函数f(x)的单调减区间.
(3)求函数取最小值时x的值.
解:(1)∵f(x)=sin2x+ sinxcosx-
sinxcosx-
= +
+ sin2x-
sin2x-
= sin2x-
sin2x- cos2x
cos2x
=sin(2x- )
)
∴其最小正周期T= =π
=π
(2)由2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
得:kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,
∴函数f(x)的单调减区间为[kπ+ ,kπ+
,kπ+ ](k∈Z)
](k∈Z)
(3)由2x- =2kπ-
=2kπ- ,k∈Z得:
,k∈Z得:
x=kπ- ,k∈Z.
,k∈Z.
∴函数取最小值时x的值为:x=kπ- ,k∈Z
,k∈Z
分析:(1)利用降幂公式与辅助角公式将f(x)=sin2x+ sinxcosx-
sinxcosx- 转化为f(x)=sin(2x-
转化为f(x)=sin(2x- ),即可求其周期;
),即可求其周期;
(2)利用正弦函数的单调性,通过整体代换即可求得函数f(x)的单调减区间;
(3)利用正弦函数的性质,由2x- =2kπ-
=2kπ- ,k∈Z即可求得函数取最小值时x的值.
,k∈Z即可求得函数取最小值时x的值.
点评:本题考查两角和与差的正弦函数,考查正弦函数的单调性,考查分析与运算能力,属于中档题.
 sinxcosx-
sinxcosx-
=
 +
+ sin2x-
sin2x-
=
 sin2x-
sin2x- cos2x
cos2x=sin(2x-
 )
)∴其最小正周期T=
 =π
=π(2)由2kπ+
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,得:kπ+
 ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,∴函数f(x)的单调减区间为[kπ+
 ,kπ+
,kπ+ ](k∈Z)
](k∈Z)(3)由2x-
 =2kπ-
=2kπ- ,k∈Z得:
,k∈Z得:x=kπ-
 ,k∈Z.
,k∈Z.∴函数取最小值时x的值为:x=kπ-
 ,k∈Z
,k∈Z分析:(1)利用降幂公式与辅助角公式将f(x)=sin2x+
 sinxcosx-
sinxcosx- 转化为f(x)=sin(2x-
转化为f(x)=sin(2x- ),即可求其周期;
),即可求其周期;(2)利用正弦函数的单调性,通过整体代换即可求得函数f(x)的单调减区间;
(3)利用正弦函数的性质,由2x-
 =2kπ-
=2kπ- ,k∈Z即可求得函数取最小值时x的值.
,k∈Z即可求得函数取最小值时x的值.点评:本题考查两角和与差的正弦函数,考查正弦函数的单调性,考查分析与运算能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 设函数
设函数