题目内容
已知函数y= 的定义域为M,
的定义域为M,
(1)求M;
(2)当x∈M时,-2x+2+3×4x≥k恒成立,求k的取值范围.
解:(1)由 ,得
,得 ,解得-1≤x<1,
,解得-1≤x<1,
所以M={x|-1≤x<1};
(2)-2x+2+3×4x=-4•2x+3•(2x)2,
令t=2x,因为x∈M,所以t∈[ ,2),
,2),
则-4•2x+3•(2x)2=3t2-4t=3 ,
,
所以当t= 即x=
即x=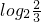 时,-2x+2+3×4x取得最小值-
时,-2x+2+3×4x取得最小值- ,
,
-2x+2+3×4x≥k恒成立,等价于- ≥k,
≥k,
所以实数k的取值范围是k ;
;
分析:(1)要使函数有意义,须有 ,解出可得M;
,解出可得M;
(2)x∈M时,-2x+2+3×4x≥k恒成立,等价于-2x+2+3×4x的最小值大于等于k,通过换元借助二次函数的性质可求得-2x+2+3×4x的最小值;
点评:本题考查函数恒成立问题、不等式的求解,考查转化思想,考查学生解决问题的能力.
 ,得
,得 ,解得-1≤x<1,
,解得-1≤x<1,所以M={x|-1≤x<1};
(2)-2x+2+3×4x=-4•2x+3•(2x)2,
令t=2x,因为x∈M,所以t∈[
 ,2),
,2),则-4•2x+3•(2x)2=3t2-4t=3
 ,
,所以当t=
 即x=
即x=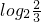 时,-2x+2+3×4x取得最小值-
时,-2x+2+3×4x取得最小值- ,
,-2x+2+3×4x≥k恒成立,等价于-
 ≥k,
≥k,所以实数k的取值范围是k
 ;
;分析:(1)要使函数有意义,须有
 ,解出可得M;
,解出可得M;(2)x∈M时,-2x+2+3×4x≥k恒成立,等价于-2x+2+3×4x的最小值大于等于k,通过换元借助二次函数的性质可求得-2x+2+3×4x的最小值;
点评:本题考查函数恒成立问题、不等式的求解,考查转化思想,考查学生解决问题的能力.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 的定义域是A,函数y=
的定义域是A,函数y=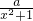 (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围. 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围. 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.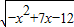 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.