题目内容
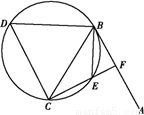
如图，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC．过点A 做圆的切线与DB的延长线交于点E，AD与BC交于点F．若AB=AC，AE=6，BD=5，则线段CF的长为______．
如图连结圆心O与A，因为过点A作圆的切线与CB的延长线交于点E．所以OA⊥AE，
因为AB=AC，AE=6，BD=5，
梯形ABCD中，AC∥BD，BD=5，
由切割线定理可知：AE2=EB•ED=EB（EB+BD），所以EB=4，
AC∥BD，则AC∥BE，EB=AC
可得四边形AEBC是平行四边形，所以AC=AB=4，BC=6．
△AFC∽△DFB，
=
即：
=
，
CF=
，
故答案为：
．
因为AB=AC，AE=6，BD=5，
梯形ABCD中，AC∥BD，BD=5，
由切割线定理可知：AE2=EB•ED=EB（EB+BD），所以EB=4，
AC∥BD，则AC∥BE，EB=AC
可得四边形AEBC是平行四边形，所以AC=AB=4，BC=6．
△AFC∽△DFB，
| AC |
| BD |
| CF |
| FB |
即：
| 4 |
| 5 |
| CF |
| 6-CF |
CF=
| 8 |
| 3 |
故答案为：
| 8 |
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2013•天津）如图，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC．过点A 做圆的切线与DB的延长线交于点E，AD与BC交于点F．若AB=AC，AE=6，BD=5，则线段CF的长为
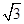,延长CE交AB于点F,求△BCF外接圆的半径.