题目内容
已知 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为坐标原点,点
为坐标原点,点 在椭圆上,且
在椭圆上,且 ,⊙
,⊙ 是以
是以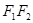 为直径的圆,直线
为直径的圆,直线 :
: 与⊙
与⊙ 相切,并且与椭圆交于不同的两点
相切,并且与椭圆交于不同的两点

(1)求椭圆的标准方程;
(2)当 ,且满足
,且满足 时,求弦长
时,求弦长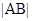 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)求椭圆的标准方程,可利用待定系数法,求出 的值即可,由已知
的值即可,由已知 ,得
,得 ,可得
,可得 ,把
,把 代入椭圆的方程,即可求出
代入椭圆的方程,即可求出 的值,从而得椭圆的标准方程;(2)当
的值,从而得椭圆的标准方程;(2)当 ,且满足
,且满足 时,求弦长
时,求弦长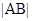 的取值范围,可利用弦长公式来求,设
的取值范围,可利用弦长公式来求,设 ,由
,由 ,得
,得 ,得
,得 ,由于同时含有
,由于同时含有 ,可消元,由直线
,可消元,由直线 :
: 与⊙
与⊙ 相切,可得
相切,可得 ,这样由弦长公式得
,这样由弦长公式得
 ,可求出
,可求出 的范围即可,由已知
的范围即可,由已知 ,且满足
,且满足 ,由
,由 ,可得
,可得 ,从而得
,从而得 的范围,进而得弦长
的范围,进而得弦长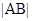 的取值范围.
的取值范围.
试题解析:(1)依题意,可知 ,∴
,∴ ,
,
解得
∴椭圆的方程为 5分
5分
(2)直线 :
: 与⊙
与⊙ 相切,
相切,
则 ,即
,即 , 6分
, 6分
由 ,得
,得 ,
,
∵直线 与椭圆交于不同的两点
与椭圆交于不同的两点
设 ∴
∴ ,
,
 ,
,
∴ .9分
.9分
∴ ∴
∴ ,
,
∴
 .11分
.11分
设 ,
,
则 ,
,
∵ 在
在 上单调递增∴
上单调递增∴ 13分
13分
考点:椭圆的方程,直线与二次曲线的位置关系.

练习册系列答案
相关题目
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
 ,且
,且 .
. 的轨迹
的轨迹 的方程;
的方程; ,若斜率为
,若斜率为 的直线
的直线 过点
过点 并与轨迹
并与轨迹 ,且对于轨迹
,且对于轨迹 ,都存在
,都存在 ,使得
,使得 成立,试求出满足条件的实数
成立,试求出满足条件的实数 的值.
的值. .
.
 直线
直线 与抛物线
与抛物线 没有交点;
没有交点; 方程
方程 表示椭圆;若
表示椭圆;若 为真命题,试求实数
为真命题,试求实数 的取值范围.
的取值范围. +
+ =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.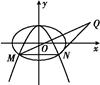

 的距离比到y轴的距离大
的距离比到y轴的距离大 .记点P的轨迹为曲线C.
.记点P的轨迹为曲线C.