题目内容
命题p:实数x满足x2-4ax+3a2<0,其中a<0;命题q:实数x满足x2-x-6≤0或x2+2x-8>0;若¬p是¬q的必要不充分条件,求a的取值范围.
x2-4ax+3a2=0对应的根为a,3a;
由于a<0,
则x2-4ax+3a2<0的解集为(3a,a),
故命题p成立有x∈(3a,a);
由x2-x-6≤0得x∈[-2,3],
由x2+2x-8>0得x∈(-∞,-4)∪(2,+∞),
故命题q成立有x∈(-∞,-4)∪[-2,+∞).
若?p是?q的必要不充分条件,即p是q的充分不必要条件,
因此有(3a,a)⊆(-∞,-4)或(3a,a)⊆[-2,+∞),
又a<0,解得a≤-4或-
≤a<0;
故a的范围是a≤-4或-
≤a<0.
由于a<0,
则x2-4ax+3a2<0的解集为(3a,a),
故命题p成立有x∈(3a,a);
由x2-x-6≤0得x∈[-2,3],
由x2+2x-8>0得x∈(-∞,-4)∪(2,+∞),
故命题q成立有x∈(-∞,-4)∪[-2,+∞).
若?p是?q的必要不充分条件,即p是q的充分不必要条件,
因此有(3a,a)⊆(-∞,-4)或(3a,a)⊆[-2,+∞),
又a<0,解得a≤-4或-
| 2 |
| 3 |
故a的范围是a≤-4或-
| 2 |
| 3 |

练习册系列答案
相关题目
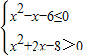 .
.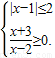
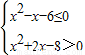 .
.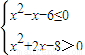 .
.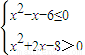 .
.