Question

11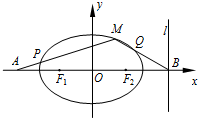．在平面直角坐标系xOy中，设中心在坐标原点的椭圆C的左、右焦点分别为F₁、F₂，右准线l：x=m+1与x轴的交点为B，BF₂=m．
（1）已知点（$\frac{\sqrt{6}}{2}$，1）在椭圆C上，求实数m的值；
（2）已知定点A（-2，0）．
①若椭圆C上存在点T，使得$\frac{TA}{TF1}$=$\sqrt{2}$，求椭圆C的离心率的取值范围；
②当m=1时，记M为椭圆C上的动点，直线AM，BM分别与椭圆C交于另一点P，Q，若$\overrightarrow{AM}$=λ$\overrightarrow{AP}$，$\overrightarrow{BM}$=μ$\overrightarrow{BQ}$，求证：λ+μ为定值．

Answer 1

分析 （1）由椭圆的准线方程列式求解．
（2）①设点T（x，y）由$\frac{TA}{T{F}_{1}}=\sqrt{2}$，得（x+2）²+y²=2[（x+1）²+y²]，即x²+y²=2．得出关于m的关系式求得离心率范围．
②设M（x₀，y₀），P（x₁，y₁），Q（x₂，y₂）由$\overrightarrow{AM}$=λ$\overrightarrow{AP}$，$\overrightarrow{BM}$=μ$\overrightarrow{BQ}$的关系列式求解．

解答 解：（1）设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$
由题意得$\left\{\begin{array}{l}{\frac{{a}^{2}}{c}=m+1}\\{（m+1）-c=m}\end{array}\right.$解得$\left\{\begin{array}{l}{{a}^{2}=m+1}\\{{b}^{2}=m}\\{c=1}\end{array}\right.$
所以椭圆方程为$\frac{{x}^{2}}{m+1}+\frac{{y}^{2}}{m}=1$
因为椭圆C过点（$\frac{\sqrt{6}}{2}，1$），所以$\frac{3}{2（m+1）}+\frac{1}{m}=1$，
解得m=2或m=$-\frac{1}{2}$（舍去）
所以m=2…4分
（2）①设点T（x，y）
由$\frac{TA}{T{F}_{1}}=\sqrt{2}$，得（x+2）²+y²=2[（x+1）²+y²]，即x²+y²=2…6分
由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=2}\\{\frac{{x}^{2}}{m+1}+\frac{{y}^{2}}{m}=1}\end{array}\right.$得y²=m²-m
因此0≤m²-m≤m，解得1≤m≤2
所以椭圆的离心率$e=\frac{1}{\sqrt{m+1}}∈[\frac{\sqrt{3}}{3}，\frac{\sqrt{2}}{2}]$…10分
②（方法一）设M（x₀，y₀），P（x₁，y₁），Q（x₂，y₂）
则$\overrightarrow{AM}=（{x}_{0}+2，{y}_{0}），\overrightarrow{AP}=（{x}_{1}+2，{y}_{1}）$
由$\overrightarrow{AM}=λ\overrightarrow{AP}$，得$\left\{\begin{array}{l}{{x}_{0}+2=λ（{x}_{1}+2）}\\{{y}_{0}=λ{y}_{1}}\end{array}\right.$
从而$\left\{\begin{array}{l}{{x}_{0}=λ{x}_{1}+2（λ-1）}\\{{y}_{0}=λ{y}_{1}}\end{array}\right.$…12分
因为$\frac{{x}_{0}^{2}}{2}{+y}_{0}^{2}=1$，所以$\frac{[λ{x}_{1}+2（λ-1）]^{2}}{2}+（λ{y}_{1}）^{2}=1$
即${λ}^{2}（\frac{{x}_{{1}^{2}}}{2}{+y}_{1}^{2}）+2（λ-1）{x}_{1}+2（λ-1）^{2}-1=0$
因为$\frac{{x}_{1}^{2}}{2}+{y}_{1}^{2}=1$，代入得$2λ（λ-1）{x}_{1}+3{λ}^{2}-4λ+1=0$
由题意知，λ≠1
故${x}_{1}=-\frac{3λ-1}{2λ}$，所以${x}_{0}=\frac{λ-3}{2}$
同理可得${x}_{0}=\frac{-μ+3}{2}$
因此$\frac{λ-3}{2}=\frac{-μ+3}{2}$
所以λ+μ=6…16分
（方法二）设M（x₀，y₀），P（x₁，y₁），Q（x₂，y₂）
直线AM的方程为$y=\frac{{y}_{0}}{{x}_{0}+2}（x+2）$
将$y=\frac{{y}_{0}}{{x}_{0}+2}（x+2）\\;\\;\\;\\;\\;代入$代入$\frac{{x}^{2}}{2}+{y}^{2}=1$，得$（\frac{1}{2}（{x}_{0}+2）^{2}+{y}_{0}^{2}）{x}^{2}+4{y}_{0}^{2}x+4{y}_{0}^{2}$-$（{x}_{0}+2）^{2}=0（*）$
因为${x}_{0}{x}_{1}=-\frac{3{x}_{0}^{2}+4{x}_{0}}{2x0+3}$，所以${x}_{1}=-\frac{3{x}_{0}+4}{2{x}_{0}+3}$，
同理${x}_{2}=\frac{3{x}_{0}-4}{2{x}_{0}-3}$…14分
因为$\overrightarrow{AM}=λ\overrightarrow{AP}，\overrightarrow{BM}=μ\overrightarrow{BQ}$
所以$λ+μ=\frac{{x}_{0}+2}{{x}_{1}+2}+\frac{{x}_{0}-2}{{x}_{1}-2}=\frac{{x}_{0}+2}{-\frac{3{x}_{0}+4}{2{x}_{0}+3}+2}+\frac{{x}_{0}-2}{\frac{3{x}_{0}-4}{2{x}_{0}-3}-2}$
=$\frac{（{x}_{0}+2）（{x}_{0}+3）}{{x}_{0}+2}+\frac{（{x}_{0}-2）（2{x}_{0}-3）}{-{x}_{0}+2}=6$
即λ+μ=6为定值…16分

点评 本题主要考查直线与圆锥曲线的位置关系在向量中的应用，属于难度较大的题目，在高考中属于压轴题目．