题目内容

20.在m(m≥2)个不同数的排列p₁p₂…p_m中，若1≤i＜j≤m时p_i＞p_j (即前面某数大于后面某数)，则称

与

构成一个逆序．一个排列的全部逆序的总数称为该排列的逆序数．记排列(n+1)n(n-1)…321的逆序数为

，如排列21的逆序数

=1，排列321的逆序数

=3，排列4321的逆序数

=6．

(Ⅰ)求、，并写出的表达式；

(Ⅱ)令=,证明 2n＜++…+＜2n+3， n=1，2，…．

（Ⅰ）由已知得a₄=10，a₅=15，

a_n=n+（n-1）+…+2+1=.

（Ⅱ）因为b_n==＞2=2，n=1，2，…，

所以b₁+b₂+…+b_n＞2n.

又因为b_n==2+，n=1，2，…，

所以b₁+b₂+…+b_n=2n+2［（）+（）+…+（）］

=2n+3-＜2n+3.

综上，2n＜b₁+b₂+…+b_n＜2n+3，n=1，2，….

练习册系列答案

学考新视野系列答案

学考英语阅读理解与完形填空系列答案

学考精练百分导学系列答案

学考传奇系列答案

学海乐园系列答案

星级口算天天练系列答案

世纪金榜初中全程复习方略系列答案

芒果教辅达标测试卷系列答案

轻松28套阳光夺冠系列答案

新优化设计系列答案

相关题目

在m(m≥2)个不同数的排列P₁P₂…P_m中，若1≤i＜j≤m时，P_i＞P_j(即前面某数大于后面某数)，则称P_i与P_j构成一个逆序．一个排列的全部逆序的总数称为该排列的逆序数．记排列(n＋1)n(n－1)…321的逆序数为a_n，例如排列21的逆序数a₁＝1，排列321的逆序数a₂＝3，排列4321的逆序数a₃＝6．

(1)求a₄、a₅，并写出a_n的表达式；

(2)令，证明：2n＜b₁＋b₂＋…＋b_n＜2n＋3，n＝1，2，…．

（理科）已知函数f（x）=alnx-ax-3（a∈R）．
（1）讨论函数f（x）的单调性；
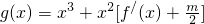（2）若函数y=f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，对任意的t∈[1，2]，若函数 $数学公式$ 在区间（t，3）上有最值，求实数m取值范围；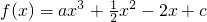
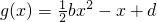（3）求证：ln（2²+1）+ln（3²+1）+ln（4²+1）+…+ln（n²+1）＜1+2lnn!（n≥2，n∈N^*）
（文科）已知函数 $数学公式$
（1）若x=-1是f（x）的极值点且f（x）的图象过原点，求f（x）的极值；
（2）若 $数学公式$ ，在（1）的条件下，是否存在实数b，使得函数g（x）的图象与函数f（x）的图象恒有含x=-1的三个不同交点？若存在，求出实数b的取值范围；否则说明理由．

在m(m≥2)个不同数的排列P₁P₂…P_m中,若1≤i＜j≤m时,P_i＞P_j,则称P_i与P_j构成一个逆序.一个排列的全部逆序的总数称为该排列的逆序数.记排列(n+1)n(n-1)…321的逆序数为a_n,如排列21的逆序数a₁=1,排列321的逆序数a₂=3,

排列4321的逆序数a₃=6.

(1) 求a₄,a₅并写出a_n的表达式;

(2)令b_n=,证明2n＜b₁+b₂+…+b_n＜2n+3,n=1,2,….

在m(m≥2)个不同数的排列p₁p₂…p_n中，若1≤i＜j≤m时p_i＞p_j(即前面某数大于后面某数)，则称p_i与p_j构成一个逆序，一个排列的全部逆序的总数称为该排列的逆序数.记排列(n+1)n(n-1)…321的逆序数为a_n.如排列21的逆序数a₁=1，排列321的逆序数a₂=3，排列4321的逆序数a₃=6.

(1)求a₄、a₅，并写出a_n的表达式；

(2)令b_n=+，证明2n＜b₁+b₂+…+b_n＜2n+3,n=1,2,3….