Question

如图，四棱锥P-ABCD的底面ABCD是平行四边形，侧面△PBC是等边三角形，且平面PBC⊥平面ABCD，∠ABC=45°，AB=，BC=4，E、F分别为PB、PA的中点．

(1)求异面直线BC与PA所成的角；

(2)求二面角P-EC-D的大小；

(3)求点A到截面EFDC的距离．

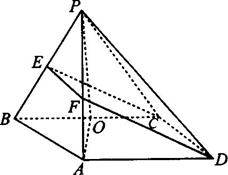
第19题图

Answer 1

答案：(1)如图所示，取BC的中点0，在△ABO中，得AO=2，知AO⊥BC，又PO⊥BC，∴BC⊥平面PAO，

∴BC⊥PA，即BC与PA所成的角为90°．

第19题图

(2)以向量、、分别为x轴、y轴、z轴建立空间直角坐标，则A(2，0，0)，B(0，-2，0)，C(0，2，0)，P(0，0，)，E(0，-1，)

∵平面PEC的法向量为=(1，0，0)，

设平面ECD的法向量为n=(x，y，z)，

则n·=0，即z=                                                        ①

n·=0，即x+y=0                                                            ②

由①②，令y=1，得n=(-1，1，)，

∴cos＜，n＞=,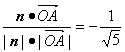

故二面角P-EC-D的大小是arccos.

(3)∵=(0，-4，0)，则A到平面EFDC的距离

d=.