题目内容
样本（x1，x2…，xn）的平均数为x，样本（y1，y2，…，yn）的平均数为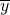
（
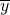≠）．若样本（x1，x2…，xn，y1，y2，…，yn）的平均数
=α+（1-α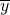），其中0＜α＜
，则n，m的大小关系为
- A.n＜m
- B.n＞m
- C.n=m
- D.不能确定
A
分析：通过特殊值判断α的范围，是否满足题意即可得到选项．
解答：法一：不妨令n=4，m=6，设样本（x1，x2…，xn）的平均数为x=6，样本（y1，y2，…，yn）的平均数为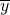=4，
所以样本（x1，x2…，xn，y1，y2，…，yn）的平均数=α+（1-α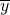）=6α+（1-α）4=
，
解得α=0.4，满足题意．
故选A．
解法二：依题意nx+my=（m+n）[ax+（1-a）y]，
∴n（x-y）=a（m+n）（x-y），x≠y，
∴a=
∈（0，），m，n∈N+，
∴2n＜m+n，
∴n＜m．
故选A．
点评：本题考查众数、中位数、平均数，考查计算能力，特殊值法是解题的常用方法．
分析：通过特殊值判断α的范围，是否满足题意即可得到选项．
解答：法一：不妨令n=4，m=6，设样本（x1，x2…，xn）的平均数为x=6，样本（y1，y2，…，yn）的平均数为
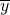=4，所以样本（x1，x2…，xn，y1，y2，…，yn）的平均数
=α+（1-α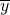）=6α+（1-α）4=，解得α=0.4，满足题意．
故选A．
解法二：依题意nx+my=（m+n）[ax+（1-a）y]，
∴n（x-y）=a（m+n）（x-y），x≠y，
∴a=
∈（0，），m，n∈N+，∴2n＜m+n，
∴n＜m．
故选A．
点评：本题考查众数、中位数、平均数，考查计算能力，特殊值法是解题的常用方法．
练习册系列答案
天天向上口算本系列答案
相关题目
已知两组样本数据x1，x2，…xn的平均数为h，y1，y2，…ym的平均数为k，则把两组数据合并成一组以后，这组样本的平均数为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
给出下列命题：
（1）函数y=sinx+
cosx的图象可由y=sinx的图象平移得到；
（2） 已知非零向量
、
，则向量
在向量
的方向上的投影可以是
•
；
（3）在空间中，若角α的两边分别与角β的两边平行，则α=β；
（4）从总体中通过科学抽样得到样本数据x1、x2、x3…xn（n≥2，n∈N+），则数值S=
（
为样本平均值）可作为总体标准差的点估计值．则上述命题正确的序号是[答]（ ）
（1）函数y=sinx+
| 3 |
（2） 已知非零向量
| a |
| b |
| a |
| b |
| a |
| ||
|
|
（3）在空间中，若角α的两边分别与角β的两边平行，则α=β；
（4）从总体中通过科学抽样得到样本数据x1、x2、x3…xn（n≥2，n∈N+），则数值S=
|
. |
| x |
| A、（1）、（2）、（4） |
| B、（4） |
| C、（2）、（3） |
| D、（2）、（4） |
某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验．选取两大块地，每大块地分成n小块地，在总共2n小块地中，随机选n小块地种植品种甲，另外n小块地种植品种乙．
（I）假设n=4，在第一大块地中，种植品种甲的小块地的数目记为X，求X的分布列和数学期望；
（II）试验时每大块地分成8小块，即n=8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量（单位：kg/hm2）如下表：
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？
附：样本数据x1，x2，…，xa的样本方差s2=
[（x1-
）2+（x1-
）2+…+（xn-
）2]，其中
为样本平均数．
（I）假设n=4，在第一大块地中，种植品种甲的小块地的数目记为X，求X的分布列和数学期望；
（II）试验时每大块地分成8小块，即n=8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量（单位：kg/hm2）如下表：
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
附：样本数据x1，x2，…，xa的样本方差s2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
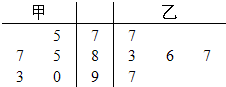（2012•江门一模）甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示．