题目内容
某公司生产一种产品的固定成本(即固定投入)为0．5万元，但每生产100件需要增加投入0．25万元，市场对此产品的需要量为500件，销售收入为函数为R(x)=5x-
(0≤x≤5)，其中x是产品售出的数量(单位：百件)． (1)把利润表示为年产量的函数f(x)．(2)年产量是多少时，当年公司所得利润最大? (3)年产量是多少时，当年公司不亏本?(取
=4．65)．
即年产量是475件时，当年公司所得利润最大．
(3)当0≤x≤5时，由f(x)≥0，-
(x-4.75)2+
≥0
∴0．1≤x≤5．(ⅱ)当x>5时，12-0．25x≥0
5<x<48． 综合得0．1≤x≤48．
即生产量在10件到4800件不亏本．
专家会诊
与函数有关的应用题经常涉及到物价、路程、产值、环保、税收、市场信息等实际问题，也可涉及角度、面积、体积、造价的最优化问题，解答这类问题的关键是建立相关函数的解析式，然后应用函数知识加以解决.在求得数学模型的解后应回到实际问题中去，看是否符合实际问题.
练习册系列答案
相关题目
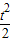（0≤t≤5），其中t为产品售出的数量（单位：百件）．
（0≤t≤5），其中t为产品售出的数量（单位：百件）．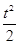
(0≤t≤5)，其中t为产品售出的数量(单位：百件).