题目内容
函数f(x)=ax3+bx2+cx+d(a≠0)是单调增函数,则下列式中成立的是
- A.a>0,b2+3ac≥0
- B.a>0,b2-3ac≤0
- C.a<0,b2+3ac≥0
- D.a<0,b2-3ac≤0
B
分析:根据导数与函数的关系进行求解,函数f(x)=ax3+bx2+cx+d(a≠0)是单调增函数,可以令f′(x)>0,从而进行求解;
解答:∵函数f(x)=ax3+bx2+cx+d(a≠0)是单调增函数,
∴f′(x)=3ax2+2bx+c≥0,在x∈R上恒成立,必须有开口向上,
可得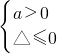 ,
,
解得a>0,(2b)2-4×(3a)c≤0,
即b2-3ac≤0,
故选B;
点评:此题主要考查函数的单调性与导数的关系,是一道基础题,解题的过程中用到了转化的思想;
分析:根据导数与函数的关系进行求解,函数f(x)=ax3+bx2+cx+d(a≠0)是单调增函数,可以令f′(x)>0,从而进行求解;
解答:∵函数f(x)=ax3+bx2+cx+d(a≠0)是单调增函数,
∴f′(x)=3ax2+2bx+c≥0,在x∈R上恒成立,必须有开口向上,
可得
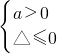 ,
,解得a>0,(2b)2-4×(3a)c≤0,
即b2-3ac≤0,
故选B;
点评:此题主要考查函数的单调性与导数的关系,是一道基础题,解题的过程中用到了转化的思想;

练习册系列答案
相关题目