题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,设向量 =(a,cosB),
=(a,cosB), =(b,cosA)且
=(b,cosA)且 ∥
∥ ,
, ≠
≠ .
.
(1)求角C的大小;
(2)求sinA+sinB的取值范围.
 =(a,cosB),
=(a,cosB), =(b,cosA)且
=(b,cosA)且 ∥
∥ ,
, ≠
≠ .
.(1)求角C的大小;
(2)求sinA+sinB的取值范围.
解:(1)∵向量 =(a,cosB),
=(a,cosB), =(b,cosA),且
=(b,cosA),且 ∥
∥ ,
,
∴a:b=cosB:cosA,即acosA=bcosB,
根据正弦定理化简得:2RsinAcosA=2RsinBcosB,即sin2A=sin2B,
∵0<2A<2π,0<2B<2π,
∴2A=2B或2A+2B=π,
又 ≠
≠  ,故A≠B,
,故A≠B,
∴A+B=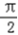 ,则C=
,则C= 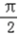 ;
;
(2)∵A+B=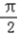 ,
,
∴sinA+sinB=sinA+sin(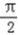 ﹣A)=sinA+cosA=
﹣A)=sinA+cosA= 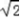 sin(A+
sin(A+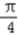 ),
),
又0<A<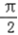 ,∴
,∴ 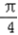 <A+
<A+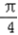 <
< ,
,
∴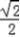 <sin(A+
<sin(A+ 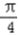 )≤1,
)≤1,
∴1<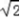 sin(A+
sin(A+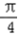 )≤
)≤ 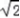 ,
,
则sinA+sinB的取值范围是(1,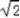 ].
].
 =(a,cosB),
=(a,cosB), =(b,cosA),且
=(b,cosA),且 ∥
∥ ,
, ∴a:b=cosB:cosA,即acosA=bcosB,
根据正弦定理化简得:2RsinAcosA=2RsinBcosB,即sin2A=sin2B,
∵0<2A<2π,0<2B<2π,
∴2A=2B或2A+2B=π,
又
 ≠
≠  ,故A≠B,
,故A≠B,∴A+B=
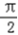 ,则C=
,则C= 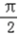 ;
;(2)∵A+B=
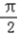 ,
, ∴sinA+sinB=sinA+sin(
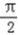 ﹣A)=sinA+cosA=
﹣A)=sinA+cosA= 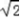 sin(A+
sin(A+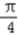 ),
),又0<A<
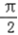 ,∴
,∴ 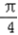 <A+
<A+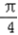 <
< ,
, ∴
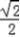 <sin(A+
<sin(A+ 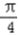 )≤1,
)≤1, ∴1<
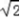 sin(A+
sin(A+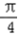 )≤
)≤ 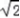 ,
,则sinA+sinB的取值范围是(1,
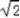 ].
].
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |