题目内容
函数f（x）对于任意的x∈R，都有f（x+1）=2f（x），当0≤x≤1时，f（x）=x（1-x），则f（-1.5）=
- A.
- B.
- C.
- D.
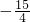
A
分析：由已知中，分别令x=-1.5，x=-0.5，结合当0≤x≤1时，f（x）=x（1-x），递推可得答案．
解答：∵函数f（x）对于任意的x∈R，都有f（x+1）=2f（x），
令x=-1.5，则f（-0.5）=2f（-1.5），
令x=-0.5，则f（0.5）=2f（-0.5），
又∵当0≤x≤1时，f（x）=x（1-x），
∴f（0.5）=0.5•0.5=
则f（-0.5）=，f（-1.5）=
故选A
点评：本题考查的知识点是抽象函数及其应用，函数的值，其中根据已知条件利用“凑配法”确定未知函数值与已知函数值之间的关系，是解答本题的关键．本题赋值巧妙恰当，是一个值得借鉴的经验
分析：由已知中，分别令x=-1.5，x=-0.5，结合当0≤x≤1时，f（x）=x（1-x），递推可得答案．
解答：∵函数f（x）对于任意的x∈R，都有f（x+1）=2f（x），
令x=-1.5，则f（-0.5）=2f（-1.5），
令x=-0.5，则f（0.5）=2f（-0.5），
又∵当0≤x≤1时，f（x）=x（1-x），
∴f（0.5）=0.5•0.5=
则f（-0.5）=
，f（-1.5）=故选A
点评：本题考查的知识点是抽象函数及其应用，函数的值，其中根据已知条件利用“凑配法”确定未知函数值与已知函数值之间的关系，是解答本题的关键．本题赋值巧妙恰当，是一个值得借鉴的经验
练习册系列答案
阅读快车系列答案
相关题目