题目内容
设函数f(x)=lnx﹣x+1,
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求证:lnx≤x﹣1;
(Ⅲ)证明: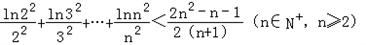
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求证:lnx≤x﹣1;
(Ⅲ)证明:
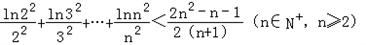
解:(Ⅰ)由已知得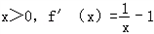 ,
,
由f'(x)>0,得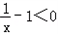 ,
,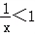 ,x>1.
,x>1.
∴f(x)在(1,+∞)上为减函数,在(0,1)为增函数.
(Ⅱ)由(Ⅰ)知:当x=1时,f(x)max=﹣1+1=0.
对任意x>0,有f(x)≤0,
即lnx﹣x+1≤0.
即lnx≤x﹣1.
(Ⅲ)由(Ⅱ)知,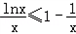 ,
,
当x≥2时,则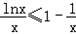 , ∴
, ∴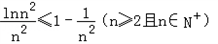 ,
,
∴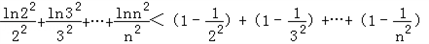 =
=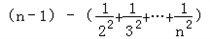 又
又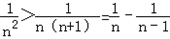 ,
,
∴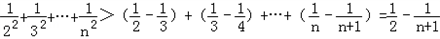
故不等式的左边小于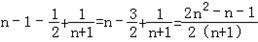 ,
,
故要证的不等式成立.
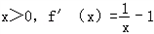 ,
,由f'(x)>0,得
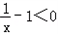 ,
,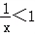 ,x>1.
,x>1. ∴f(x)在(1,+∞)上为减函数,在(0,1)为增函数.
(Ⅱ)由(Ⅰ)知:当x=1时,f(x)max=﹣1+1=0.
对任意x>0,有f(x)≤0,
即lnx﹣x+1≤0.
即lnx≤x﹣1.
(Ⅲ)由(Ⅱ)知,
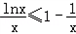 ,
,当x≥2时,则
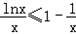 , ∴
, ∴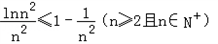 ,
,∴
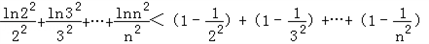 =
=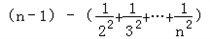 又
又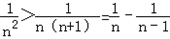 ,
, ∴
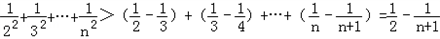
故不等式的左边小于
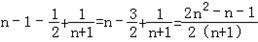 ,
,故要证的不等式成立.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目