题目内容
定义在实数集上的函数f(x)满足下列条件:
①f(x)是偶函数;②对任意非负实数x、y,都有f(x+y)=2f(x)f(y);③当x>0时,恒有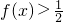 .
.
(1)求f(0)的值;
(2)证明:f(x)在[0,+∞)上是单调增函数;
(3)若f(3)=2,解关于a的不等式f(a2-2a-9)≤8.
解:(1)解:令x=0,y=1,
则f(1)=2f(0)•f(1),
∵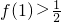 ,
,
∴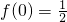 .…
.…
(2)∵当x>0时,恒有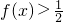 ,又f(x)是偶函数,
,又f(x)是偶函数,
∴当x<0时, ,
,
又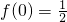 ,f(x)>0恒成立.…
,f(x)>0恒成立.…
设0≤x1<x2,则x2-x1>0, ,
,
∴f(x2)=2f(x1)f(x2-x1)>f(x1),…
∴f(x)在[0,+∞)上是单调增函数.…
(3)令x=y=3,则f(6)=2f2(3)=8,…
∴f(a2-2a-9)=f(|a2-2a-9|)≤f(6),
由f(x)在[0,+∞)上是单调增函数,
得|a2-2a-9|≤6,…
即 ,
,
解得 ,
,
∴-3≤a≤-1或3≤a≤5.…16 分
分析:(1)令x=0,y=1,易由f(x+y)=2f(x)f(y)求出f(0)的值;
(2)设0≤x1<x2,根据当x>0时,恒有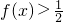 及f(x)是偶函数,结合函数单调性的定义可判断出f(x)在[0,+∞)上是单调增函数;
及f(x)是偶函数,结合函数单调性的定义可判断出f(x)在[0,+∞)上是单调增函数;
(3)令x=y=3,则f(6)=8,由(2)中函数的单调性,可将抽象不等式具体为|a2-2a-9|≤6,解绝对值不等式可得答案.
点评:本题考查的知识点是抽象函数及其应用,函数单调性的判断与证明,函数单调性的性质,熟练掌握抽象函数“凑”的思想是解答的关键,本题难度中档.
则f(1)=2f(0)•f(1),
∵
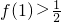 ,
,∴
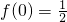 .…
.…(2)∵当x>0时,恒有
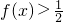 ,又f(x)是偶函数,
,又f(x)是偶函数,∴当x<0时,
 ,
,又
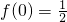 ,f(x)>0恒成立.…
,f(x)>0恒成立.…设0≤x1<x2,则x2-x1>0,
 ,
,∴f(x2)=2f(x1)f(x2-x1)>f(x1),…
∴f(x)在[0,+∞)上是单调增函数.…
(3)令x=y=3,则f(6)=2f2(3)=8,…
∴f(a2-2a-9)=f(|a2-2a-9|)≤f(6),
由f(x)在[0,+∞)上是单调增函数,
得|a2-2a-9|≤6,…
即
 ,
,解得
 ,
,∴-3≤a≤-1或3≤a≤5.…16 分
分析:(1)令x=0,y=1,易由f(x+y)=2f(x)f(y)求出f(0)的值;
(2)设0≤x1<x2,根据当x>0时,恒有
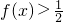 及f(x)是偶函数,结合函数单调性的定义可判断出f(x)在[0,+∞)上是单调增函数;
及f(x)是偶函数,结合函数单调性的定义可判断出f(x)在[0,+∞)上是单调增函数;(3)令x=y=3,则f(6)=8,由(2)中函数的单调性,可将抽象不等式具体为|a2-2a-9|≤6,解绝对值不等式可得答案.
点评:本题考查的知识点是抽象函数及其应用,函数单调性的判断与证明,函数单调性的性质,熟练掌握抽象函数“凑”的思想是解答的关键,本题难度中档.

练习册系列答案
相关题目