题目内容
已知函数f(x)=ax3+bx2+c(x∈R)的图像与直线15x-y+10=0切于点(-1,-5),且函数f(x)在x=4处取得极值.(Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的极值;
(Ⅲ)当x∈[-m,m]时,求f(x)最大值.
解:(1)f′(x)=3 ax2+2bx
∵f(x)的图像与直线15x-y+10=0切于点(-1,-5)
∴![]() ①
①
又f(x)在x=4处取得极值,∴48a+8b=0②
由①②得∴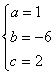
∴f(x)=x3-6x2+2
(Ⅱ)f′(x)=3x2-12x=3x(x-4)
令f′(x)=3x(x-4)=0得x=0,x=4
列表如下:
x | (-∞,0) | 0 | (0,4) | 4 | (4,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) |
| 2 |
| -30 |
|
从而当x=0时,f(x)的极大值为2
从而当x=4时,f(x)的极小值为-30
(Ⅲ)据(Ⅱ)知f(0)=2是极大值,在(4,+∞)内函数f(x)单调递增,并且可验证f(6)=2,据已知条件知m>0
当0<m≤6时,f(x)的最大值是f(0)=2
当m>6时,f(x)的最大值是m3-6m2+2

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |