题目内容
已知x,y＞0,且x+y＞2,试证:
,
中至少有一个小于2.
证明：假设都不小于2,即≥2,且
≥2.
因为x、y＞0,所以1+x≥2y,且1+y≥2x.
把这两个不等式相加,得2+x+y≥2(x+y),
从而x+y≤2.这与已知条件x+y＞2矛盾.因此
,
都不小于2是不可能的,即原命题成立.
练习册系列答案
相关题目
已知直线l过直线2x+y-5=0和直线x+2y-4=0的交点，且在两坐标轴上的截距互为相反数，则直线l的方程为（ ）
| A、x-y-1=0 | B、x+y-3=0或x-2y=0 | C、x-y-1=0或x-2y=0 | D、x+y-3=0或x-y-1=0 |
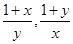中至少有一个小于2。
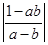>1