题目内容

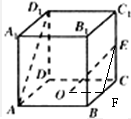
如图，在正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，E为C1C的中点，则异面直线D1A与EO所成角的余弦值为______．
取BC中点F，连结OF、EF
由正方体的性质，可得EF∥AD1，∠OEF就是异面直线D1A与EO所成角
设正方体的棱长等于2，可得
Rt△OEF中，OF=1，EF=
2

∴OE=
OF2+EF2
=
3
，cos∠OEF=
EF
OF
=
6
3

即异面直线D1A与EO所成角的余弦值为
6
3

故答案为：
6
3

练习册系列答案
相关题目
S是正△ABC所在平面外一点,且SA=SB=SC=AB,如果E、F分别为SC、AB中点,则异面直线EF与SA所成的角为(    )
A.90°          B.60°                 C.45°          D.30°
设直线平面，过平面外一点与都成角的直线有且
只有   （   ）
A．１条B．２条C．３条D．４条
三棱锥A-BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，点E、F分别在AC，AD上，使平面BEF⊥平面ACD，且EF∥CD，则平面BEF与平面BCD所成的二面角的正弦值为                  （ ）
A．B．C．D．
如图，正三棱柱ABC-A1B1C1的底面边长为1，高为h（h＞3），点M在侧棱BB1上移动，并且M到底面ABC的距离为x，且AM与侧面BCC1B1所成的角为α．
（1）若α在区间[
π
6
，
π
4
]上变化，求x的变化范围；
（2）若α为
π
6
，求AM与BC所成角的余弦值．
如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=1，则异面直线AC1与BB1所成的角为（　　）
A．arctan
2
2
3
B．arccos
2
2
3
C．arcsin
1
3
D．arctan2
2
如图，平面ABCD⊥平面ADEF，其中ABCD为矩形，ADEF为梯形，AF∥DE，AF⊥FE，AF=AD=2DE=2．
（Ⅰ）求异面直线EF与BC所成角的大小；
（Ⅱ）若二面角A-BF-D的平面角的余弦值为
1
3
，求AB的长．
正方体ABCD-A1B1C1D1棱长为2，E是棱A1B1的中点．
（1）求异面直线A1B1与BD的距离；
（2）求直线EC1与BD所成角的大小．
正四面体A-BCD中，异面直线AB与CD所成角为（　　）
A．
π
6
B．
π
4
C．
π
3
D．
π
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网