题目内容
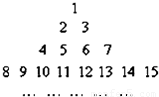
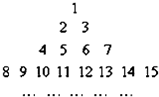 把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右第j个数.
把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右第j个数.(1)求a69的值;
(2)用i,j表示aij;
(3)记An=a11+a22+a33+…+ann(n∈N*),求证:当n≥4时,An>n+
| C | 3 n |
分析:(1)根据已知条件可知每行的正整数的个数是等比数列,据此可先算出前5行的数分别为1,2,4,8,16总共31个,从而得到a69的值;
(2)观察已知可得每行的第一个数是以1为首项,以2为公比的等比数列,从而得ai1=2i-1,每列的数又构成了以1为公差的等差数列,所以aij=2i-1+j-1,根据该通项判断300的位置
(3)利用(2)可得ann=2n-1+n-1,用分组求和,即可得到结论.
(2)观察已知可得每行的第一个数是以1为首项,以2为公比的等比数列,从而得ai1=2i-1,每列的数又构成了以1为公差的等差数列,所以aij=2i-1+j-1,根据该通项判断300的位置
(3)利用(2)可得ann=2n-1+n-1,用分组求和,即可得到结论.
解答:(1)解:由于第i行有2i-1个数,前5行共有1+2+4+8+16=31个数
所以第6行的第9个数是正整数的第40个数,a69=25+(9-1)=40…(2分)
(2)解:因为数表中前i-1行共有1+2+22+…+2i-2=2i-1-1个数,则第i行的第一个数是2i-1,
所以aij=2i-1+j-1…(5分)
(3)证明:因为aij=2i-1+j-1,则ann=2n-1+n-1(n∈N*),…(6分)
所以An=(1+2+22+…+2n-1)+[0+1+2+…+(n-1)]=2n-1+
…(8分)
当n≥4时,An=(1+1)n-1+
>
+
+
+
-1+
=n2+
.…(10分)
所以第6行的第9个数是正整数的第40个数,a69=25+(9-1)=40…(2分)
(2)解:因为数表中前i-1行共有1+2+22+…+2i-2=2i-1-1个数,则第i行的第一个数是2i-1,
所以aij=2i-1+j-1…(5分)
(3)证明:因为aij=2i-1+j-1,则ann=2n-1+n-1(n∈N*),…(6分)
所以An=(1+2+22+…+2n-1)+[0+1+2+…+(n-1)]=2n-1+
| n(n-1) |
| 2 |
当n≥4时,An=(1+1)n-1+
| n(n-1) |
| 2 |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| n(n-1) |
| 2 |
| C | 3 n |
点评:本题以表格的形式给出正整数的排序方式,其关键是由表中的排序观察总结出每行的第一个数等比的规律及每行内的数成等差的规律,从而得出任意一个数的通项公式,结合通项的特点,又考查了分组求和的方法,从而培养学生的观察、发现、总结规律的能力,综合运用公式的能力.

练习册系列答案
相关题目
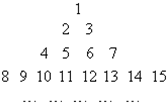 把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右第j个数.
把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右第j个数.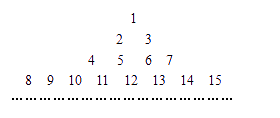
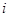 行共有
行共有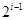 个正整数,设
个正整数,设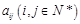 表示位于这个数表中从上往下数第
表示位于这个数表中从上往下数第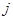 个数.
个数.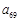 的值;
的值;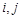 表示
表示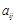 ;
;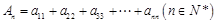 ,求证:当
,求证:当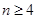 时,
时,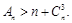
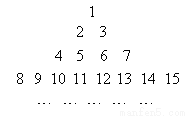
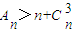 .
.