Question

求函数的导数 

Answer 1

命题意图  本题3个小题分别考查了导数的四则运算法则，复合函数求导的方法，以及抽象函数求导的思想方法  这是导数中比较典型的求导类型 

知识依托  解答本题的闪光点是要分析函数的结构和特征，挖掘量的隐含条件，将问题转化为基本函数的导数 

错解分析  本题难点在求导过程中符号判断不清，复合函数的结构分解为基本函数出差错 

技巧与方法  先分析函数式结构，找准复合函数的式子特征，按照求导法则进行求导 

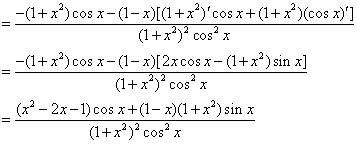
(2)解  y=μ³,μ=ax－bsin²ωx,μ=av－by

v=x,y=sinγ  γ=ωx

y′=(μ³)′=3μ²·μ′=3μ²(av－by)′

=3μ²(av′－by′)=3μ²(av′－by′γ′)

=3(ax－bsin²ωx)²(a－bωsin2ωx)

(3)解法一  设y=f(μ),μ=,v=x²+1,则

y′_x=y′_μμ′_v·v′_x=f′(μ)·v^－·2x

=f′()··2x

=

解法二  y′=［f()］′=f′()·()′

=f′()·(x²+1)·(x²+1)′

=f′()·(x²+1) ·2x

=f′()