题目内容
某食品厂为了检查一条自动包装流水线的生产情况,从该流水线上随机抽取40件产品作为样本,测得它们的重量(单位:克),将重量按如下区间分组: ,
, ,
,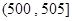 ,
, ,
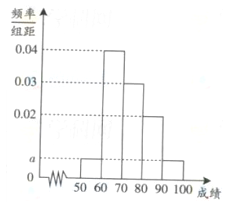
,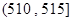 ,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
(1)在上述抽取的40件产品中任取2件,设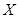 为合格产品的数量,求
为合格产品的数量,求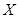 的分布列和数学期
的分布列和数学期
望 ;
;
(2)若从流水线上任取3件产品,求恰有2件合格产品的概率.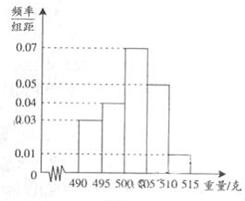
(1)参考解析;(2)
解析试题分析:(1)由于重量超过495克但不超过510克的产品为合格产品,且视频率为概率,所以根据样本的频率分布直方图可计算出合格产品的数量和不合格产品的数量.由于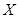 为合格产品的数量,即可得求得相应的概率,从而根据数学期望的公式,求得结论.
为合格产品的数量,即可得求得相应的概率,从而根据数学期望的公式,求得结论.
(2)由于任意抽取一件为合格品的概率为0.8.所以从流水线上任取3件产品,恰有2件合格产品的概率为 .
.
(1)由样本的频率分布直方图得,合格产品的频率为  . 2 分
. 2 分
所以抽取的40件产品中,合格产品的数量为 . 3 分
. 3 分
则 可能的取值为0,1,2, 4分
可能的取值为0,1,2, 4分
所以 ,
, ,
, ,
,
因此 的分布列为
的分布列为
7分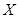
0 1 2 



故 数学期望
数学期望 . 9分
. 9分
(2)因为从流水线上任取1件产品合格的概率为 , 10分
, 10分
所以从流水线上任取3件产品,恰有2件合格产品的概率为 . 13分
. 13分
考点:1.统计的知识.2.概率的知识.3.阅读能力.

(2014·泰安模拟)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:
| 锻炼时间 (分钟) | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) |
| 人数 | 40 | 60 | 80 | 100 | 80 | 40 |
(1)其中课外体育锻炼时间在
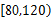 分钟内的学生应抽取多少人?
分钟内的学生应抽取多少人?(2)若从(1)中被抽取的学生中随机抽取2名,求这2名学生课外体育锻炼时间均在
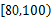 分钟内的概率.
分钟内的概率. 关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用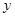 (万元),有如下的统计资料:
(万元),有如下的统计资料:
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
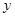 对
对 呈线形相关关系.试求:线形回归方程;(
呈线形相关关系.试求:线形回归方程;( ,
, )
)(2)估计使用年限为10年时,维修费用是多少?
某批次的某种灯泡共 个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于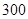 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
| 寿命(天) | 频数 | 频率 |
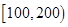 |  |  |
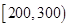 |  |  |
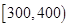 |  |  |
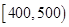 | 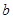 | 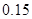 |
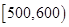 |  | 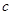 |
| 合计 |  |  |
 、
、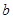 、
、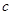 的值;
的值;(2)某人从这
 个灯泡中随机地购买了
个灯泡中随机地购买了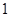 个,求此灯泡恰好不是次品的概率;
个,求此灯泡恰好不是次品的概率;(3)某人从这批灯泡中随机地购买了
 个,如果这
个,如果这 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求 的最小值.
的最小值. 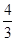 倍.
倍.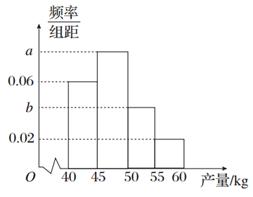
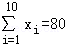 ,
, ,
, ,
,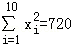 .
. ,
,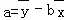 ,其中
,其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 .
.

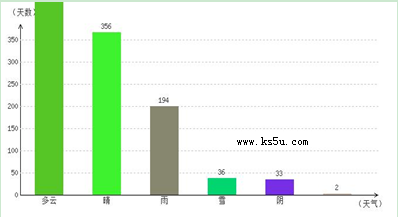
 天,晴
天,晴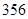 天,雨
天,雨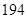 天,雪
天,雪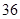 天,阴
天,阴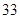 天,其它2天,合计天数为:
天,其它2天,合计天数为: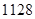 天.
天.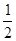 的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为
的概率乘公交或打出租的方式上班(每天一次,且交通方式仅选一种),每天交通费用相应为 元或
元或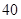 元;在非雨雪天的情况下,他以
元;在非雨雪天的情况下,他以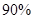 的概率骑自行车上班,每天交通费用
的概率骑自行车上班,每天交通费用 元;另外以
元;另外以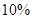 的概率打出租上班,每天交通费用
的概率打出租上班,每天交通费用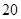 元.(以频率代替概率,保留两位小数. 参考数据:
元.(以频率代替概率,保留两位小数. 参考数据: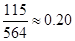 )
)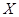 (单位:元),求
(单位:元),求


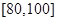 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在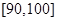 之间的概率;
之间的概率;