题目内容
设随机变量ξ服从正态分布N（u，9），若p（ξ＞3）=p（ξ＜1），则u=________．
2
分析：根据p（ξ＞3）=p（ξ＜1），由正态曲线的对称性得u=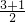
=2．
解答：∵随机变量ξ服从正态分布N（u，9），p（ξ＞3）=p（ξ＜1），
∴u=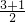=2
故答案为2
点评：本题考查正态分布，正态曲线有两个特点：（1）正态曲线关于直线x=μ对称；（2）在正态曲线下方和x轴上方范围内的区域面积为1
分析：根据p（ξ＞3）=p（ξ＜1），由正态曲线的对称性得u=
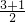=2．解答：∵随机变量ξ服从正态分布N（u，9），p（ξ＞3）=p（ξ＜1），
∴u=
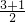=2故答案为2
点评：本题考查正态分布，正态曲线有两个特点：（1）正态曲线关于直线x=μ对称；（2）在正态曲线下方和x轴上方范围内的区域面积为1
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
设随机变量ξ服从正态分布N（0，1）Φ（x）=P（ξ＜x，则下列结论不正确的是（ ）
A、Φ(0)=
| ||
| B、Φ（x）=1-Φ（-x） | ||
| C、p（|ξ|）＜a=2Φ（a）-1（a＞1） | ||
| D、p（|ξ|＞a）=1-Φ（a）（a＞0） |
设随机变量ξ服从正态分布N（0，1），若P（ξ＞1.3）=p，则P（-1.3＜ξ＜0）=（ ）
A、
| ||
| B、1-p | ||
| C、1-2p | ||
D、
|
设随机变量ξ服从正态分布N（1，δ2），若P（ξ＞-2）=0.7，则函数f（x）=x2+4x+ξ不存在零点的概率是（ ）
| A、0.7 | B、0.8 | C、0.3 | D、0.2 |