题目内容
甲、乙、丙三名射击运动员射中目标的概率分别为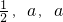 (0<a<1),三各射击一次,击中目标的次数记为X.
(0<a<1),三各射击一次,击中目标的次数记为X.
(Ⅰ)求X的分布列;
(Ⅱ)若P(X=1)的值最大,求实数a的取值范围.
解:设“甲、乙、丙三名运动员各射击一次击中目标”分别为事件A,B,C,所以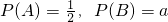 ,P(C)=a,且A,B,C相互独立.…(1分)
,P(C)=a,且A,B,C相互独立.…(1分)
(Ⅰ)X的可能取值为0,1,2,3.
所以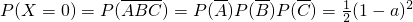 ,
,
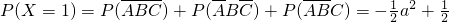 ,
,
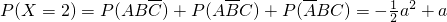 ,
,
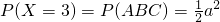 .
.
所以X的分布列为
…(4分)
(Ⅱ)因为P(ζ=1)的值最大,
所以P(X=1)-P(X=0)≥0,P(X=1)-P(X=2)≥0,P(X=1)-P(X=3)≥0.…(6分)
所以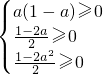 又0<a<1,
又0<a<1,
解得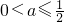 ,
,
所以a的取值范围是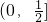 . …(10分)
. …(10分)
分析:(Ⅰ)确定X的可能取值,求出相应的概率,即可得到X的分布列;
(Ⅱ)因为P(X=1)的值最大,所以P(X=1)-P(X=0)≥0,P(X=1)-P(X=2)≥0,P(X=1)-P(X=3)≥0,由此可建立不等式组,从而可求实数a的取值范围.
点评:本题考查离散型随机变量的分布列,解题的关键是确定变量的取值,求出相应的概率.
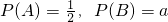 ,P(C)=a,且A,B,C相互独立.…(1分)
,P(C)=a,且A,B,C相互独立.…(1分)(Ⅰ)X的可能取值为0,1,2,3.
所以
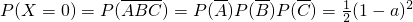 ,
,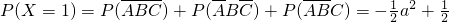 ,
,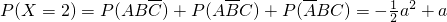 ,
,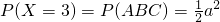 .
.所以X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | 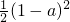 |  | 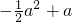 |  |
(Ⅱ)因为P(ζ=1)的值最大,
所以P(X=1)-P(X=0)≥0,P(X=1)-P(X=2)≥0,P(X=1)-P(X=3)≥0.…(6分)
所以
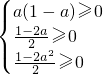 又0<a<1,
又0<a<1,解得
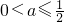 ,
,所以a的取值范围是
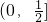 . …(10分)
. …(10分)分析:(Ⅰ)确定X的可能取值,求出相应的概率,即可得到X的分布列;
(Ⅱ)因为P(X=1)的值最大,所以P(X=1)-P(X=0)≥0,P(X=1)-P(X=2)≥0,P(X=1)-P(X=3)≥0,由此可建立不等式组,从而可求实数a的取值范围.
点评:本题考查离散型随机变量的分布列,解题的关键是确定变量的取值,求出相应的概率.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

