题目内容
(本小题共12分)数列![]() 满足
满足![]() ,(
,(![]() )
)
(Ⅰ) 当![]() 时,求
时,求![]() 及
及![]() ;
;
(Ⅱ)是否存在实数![]() ,使得数列
,使得数列![]() 为等差数列或等比数列?若存在,求出其通项公式,若不存在,说明理由;
为等差数列或等比数列?若存在,求出其通项公式,若不存在,说明理由;
解:(本小题共12分)(Ⅰ) ![]()
![]() ,故
,故![]() ,所以
,所以![]() .
.
(Ⅱ) ![]() ,
,
![]() ,
,
![]() ,
,
若数列![]() 为等差数列,则
为等差数列,则![]()
![]() 方程没有实根,故不存在
方程没有实根,故不存在![]() ,使得数列
,使得数列![]() 为等差数列.
为等差数列.
若数列![]() 为等比数列,则
为等比数列,则![]() ,即
,即![]()
解得:![]() .
.![]()
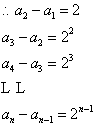 将
将![]() 个式子相加,
个式子相加,![]() ,
,
![]()
![]()
又![]() 符合条件,
符合条件,![]()
![]()
![]() ,故数列
,故数列![]() 为等比数列.通项公式为
为等比数列.通项公式为![]()

练习册系列答案
相关题目
(本小题共12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
|
月收入(单位百元) |
[15,25 |
[25,35 |
[35,45 |
[45,55 |
[55,65 |
[65,75 |
|
频数 |
5 |
10 |
15 |
10 |
5 |
5 |
|
赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
|
|
月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
赞成 |
|
|
|
|
不赞成 |
|
|
|
|
合计 |
|
|
|
(2)若对在[15,25)
,[25,35)的被调查中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为 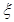 ,求随机变量
,求随机变量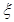 的分布列。
的分布列。
附: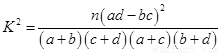
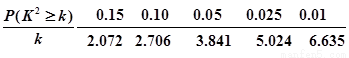
 ,项数为偶数,如果其奇数项的和为
,项数为偶数,如果其奇数项的和为 ,偶数项的和为
,偶数项的和为 ,求此数列的公比和项数.
,求此数列的公比和项数.




 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的
解 析 式;
的
解 析 式; 中,角
中,角 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.
 ,项数为偶数,如果其奇数项的和为
,项数为偶数,如果其奇数项的和为 ,偶数项的和为
,偶数项的和为 ,求此数列的公比和项数.
,求此数列的公比和项数.