题目内容
用火柴棒摆“金鱼”,按照上面的规律,第 个“金鱼”图需要火柴棒的根数为( )
个“金鱼”图需要火柴棒的根数为( )
A. | B. | C. | D. |
D
解析试题分析:第一个需8根,第二个需8+6=14(根),第三个8+6+6=20(根),需要的火柴棒根数呈等差数列,首项为8,公差为6,则第 个需
个需 (根).
(根).
考点:等差数列的通项公式.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
设等差数列{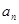 }的前n项和为Sn,若a1=1,a2+a3=11,则S6一S3=
}的前n项和为Sn,若a1=1,a2+a3=11,则S6一S3=
| A.27 | B.39 |
| C.45 | D.63 |
在等差数列{an}中,若 ,则
,则 的值为( )
的值为( )
| A.80 | B.60 | C.40 | D.20 |
设等差数列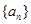 的前
的前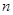 项和为
项和为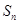 ,若
,若 ,
, ,则
,则 中最大的是()
中最大的是()
A. | B. | C. | D. |
已知 表示数列
表示数列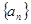 的前
的前 项的和,若对任意
项的和,若对任意 满足
满足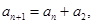 且
且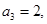
则 =( )
=( )
A.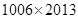 | B.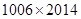 | C.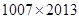 | D. |
已知等差数列{ }的前
}的前 项和为
项和为 ,且
,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知数列 是等差数列,
是等差数列,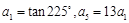 ,设
,设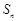 为数列
为数列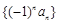 的前
的前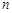 项和,则
项和,则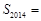 ( )
( )
| A.2014 | B.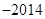 | C.3021 | D.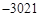 |
在等差数列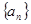 中,已知
中,已知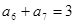 ,则
,则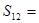 ( )
( )
A.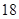 | B.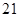 | C.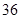 | D. |
在等差数列{an}中,已知a4+a8=16,则a2+a10=( )
| A.12 | B.16 | C.20 | D.24 |