题目内容
若二次项系数为a的二次函数
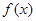 同时满足如下三个条件,求
同时满足如下三个条件,求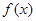 的解析式.
的解析式.①
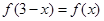 ;②
;②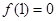 ;③对任意实数
;③对任意实数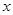 ,都有
,都有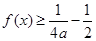 恒成立.
恒成立.(文) 设二次函数
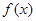 满足:(1)
满足:(1)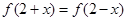 ,(2)被
,(2)被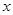 轴截得的弦长为2,(3)在
轴截得的弦长为2,(3)在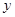 轴截距为6,求此函数解析式
轴截距为6,求此函数解析式方法一:利用
 一般解析式.设
一般解析式.设 ,
,依题意得:
 ⇒
⇒
由
 -
- ,得
,得 恒成立,
恒成立,∴
 即
即 ∴a=1,
∴a=1, ∴
∴ .
.方法二:依题意可设
 ,由
,由 ,
,  ,
,从而
 ≥
≥ -
- 恒成立,则-
恒成立,则- ≥
≥ -
- ,且a>0,
,且a>0,即+
 -
- ≤0,即
≤0,即 ≤0,a>0,∴a=1.从而
≤0,a>0,∴a=1.从而
(文)(解:根据题意可知函数对称轴为
 ,由被
,由被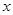 轴截得的弦长为2,可得
轴截得的弦长为2,可得 的两根
的两根 ,
, ,可设
,可设 ,由
,由 ,∴
,∴ [
[略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
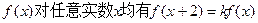 ,其中
,其中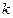 为已知的正常数,且
为已知的正常数,且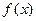 在区间[0,2]上有表达式
在区间[0,2]上有表达式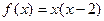 .
.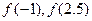 的值;
的值;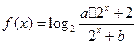 (
(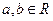 )的图象过点(1,2),它的反函数的图象也过点(1,2)。
)的图象过点(1,2),它的反函数的图象也过点(1,2)。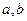 的值,并求函数
的值,并求函数 的定义域和值域;
的定义域和值域;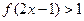 。
。 下,
下, 的象是( )
的象是( )



 ,
, ,
, ,则
,则 的大小顺序为
的大小顺序为



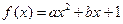 (
(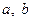 为实数,
为实数,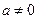 ,
,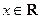 ),
),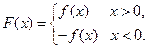
 ,且函数
,且函数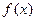 的值域为
的值域为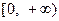 ,求
,求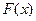 的表达式;
的表达式;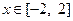 时,
时,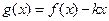 是单调函数,求实数
是单调函数,求实数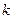 的取值范围;
的取值范围;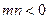 ,
,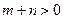 ,
,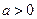 ,且函数
,且函数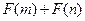 是否大于
是否大于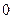 ?
? (a>0且a≠1)的反函数的图像经过点(1,4),则a=
(a>0且a≠1)的反函数的图像经过点(1,4),则a= 
 的奇偶性为
的奇偶性为