Question

设函数,的两个极值点为,

线段的中点为.

(1) 如果函数为奇函数,求实数的值;当时，求函数图象的对称中心；

(2) 如果点在第四象限,求实数的范围;

(3) 证明:点也在函数的图象上,且为函数图象的对称中心.

Answer 1

解：（1）【法一】因为为奇函数，所以,

       得：.

当时，，

有，则为奇函数.

【法二】,恒成立，

,

求得.

当时，，该图象可由奇函数的图象向

右平移一个单位得到，

可知函数图象的对称中心为（1，0）.

（2）,

令，则为两实根.

           ,.

 

=

= , 

点在第四象限,

得：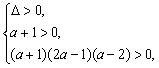 

.

（3）由（2）得点，

又

=，所以点也在函数的图象上.

【法一】设为函数的图象上任意一点，

关于的对称点为 

而

=.
即在函数的图像上.

所以，为函数的对称中心.

【法二】设 

 

                 .

为奇函数，

对称中心为.

 把函数的图象按向量

平移后得的图象，

 为函数的对称中心.

【说明】本题考查函数的奇偶性，函数图像平移，图象对称性，考查化归转化思想及运算能力.