题目内容
19．在对人们的休闲方式的一次调查中，共调查了120人，其中女性65人，男性55人．女性中有40人主要的休闲方式是看电视，另外25人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外35人主要的休闲方式是运动．则能够以多大的把握认为性别与休闲方式有关系（ ）| A． | 0.1 | B． | 0.01 | C． | 0.9 | D． | 0.99 |
分析 根据所给的数据填写列联表，计算K2，对照数表即可得出概率结论．
解答 解：根据所给的数据得到2×2列联表，如下；
| 男 | 女 | 合计 | |
| 看电视 | 20 | 40 | 60 |
| 运动 | 35 | 25 | 60 |
| 合计 | 55 | 65 | 120 |
所以有99%即（0.99）的把握认为性别与休闲方式有关系．
故选：D．
点评 本题考查了独立性检验和列联表的应用问题，正确计算出这组数据的观测值，是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
10．设n∈N*，f（n）=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$，计算得f（2）=$\frac{3}{2}$，f（4）＞2，f（8）＞$\frac{5}{2}$，f（16）＞3，观察上述结果，可推测一般结论为（ ）
| A． | f（n）≥$\frac{lo{g}_{2}n+2}{2}$（n∈N*） | B． | f（2n）≥$\frac{n+2}{2}$（n∈N*） | ||
| C． | f（2n）≥$\frac{lo{g}_{2}n+2}{2}$（n∈N*） | D． | f（2n）≥$\frac{n+2}{2}$（n∈N*） |
14．若f（x）是定义在R上的可导函数，且ef'（x）的图象如图所示，则y=f（x）的递减区间是（ ）
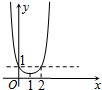
| A． | （-∞，0） | B． | （2，+∞） | C． | （0，1） | D． | （0，2） |
如图，在三棱台ABO-A1B1O1中，侧面AOO1A1与侧面OBB1O1是全等的直角梯形，且OO1⊥OB，OO1⊥OA，平面AOO1A1⊥平面OBB1O1，OB=3，O1B1=1，OO1=$\sqrt{3}$．
是
上的增函数，则实数
的取值范围是 .