题目内容
设函数f(x)=Asin(ωx+φ),(A≠0,ω>0,-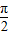 <φ<
<φ<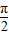 )的图象关于直线x=
)的图象关于直线x=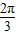 对称,它的周期是π,则( )
对称,它的周期是π,则( )A.f(x)的图象过点(0,
 )
)B.f(x)的图象在[
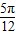 ,
,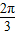 ]上递减
]上递减C.f(x)的最大值为A
D.f(x)的一个对称中心是点(
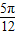 ,0)
,0)
【答案】分析:由周期公式可先求ω,根据函数对称轴处取得函数最值,由函数的图象关于直线x=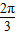 对称,可得sin(∅+
对称,可得sin(∅+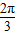 )=±1,代入可得∅=
)=±1,代入可得∅=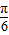 ,根据三角函数的性质逐个检验选项.
,根据三角函数的性质逐个检验选项.
解答:解:T=π,∴ω=2.
∵图象关于直线x=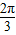 对称,
对称,
sin(φ+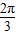 ×2)=±1
×2)=±1
即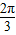 ×2+φ=
×2+φ=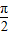 +kπ,k∈Z
+kπ,k∈Z
又∵-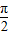 <φ<
<φ<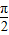 ,∴φ=
,∴φ=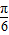
∴f(x)=Asin(2x+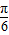 ).再用检验法逐项验证.
).再用检验法逐项验证.
故选D
点评:本题考查了三角函数的性质:周期公式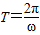 的应用;三角函数对称轴的性质,正弦函数在对称轴处取得最值.
的应用;三角函数对称轴的性质,正弦函数在对称轴处取得最值.
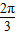 对称,可得sin(∅+
对称,可得sin(∅+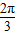 )=±1,代入可得∅=
)=±1,代入可得∅=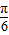 ,根据三角函数的性质逐个检验选项.
,根据三角函数的性质逐个检验选项.解答:解:T=π,∴ω=2.
∵图象关于直线x=
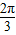 对称,
对称,sin(φ+
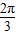 ×2)=±1
×2)=±1即
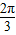 ×2+φ=
×2+φ=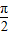 +kπ,k∈Z
+kπ,k∈Z又∵-
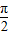 <φ<
<φ<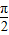 ,∴φ=
,∴φ=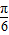
∴f(x)=Asin(2x+
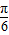 ).再用检验法逐项验证.
).再用检验法逐项验证.故选D
点评:本题考查了三角函数的性质:周期公式
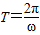 的应用;三角函数对称轴的性质,正弦函数在对称轴处取得最值.
的应用;三角函数对称轴的性质,正弦函数在对称轴处取得最值. 
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 (n∈N*)
(n∈N*) .
. 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.