题目内容
已知数列{an}的前n项和为Sn,a1= 且Sn=Sn﹣1+an﹣1+
且Sn=Sn﹣1+an﹣1+ ,数列{bn}满足b1=﹣
,数列{bn}满足b1=﹣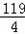
且3bn﹣bn﹣1=n(n≥2且n∈N*).
(1)求{an}的通项公式;
(2)求证:数列{bn﹣an}为等比数列;
(3)求{bn}前n项和的最小值.
 且Sn=Sn﹣1+an﹣1+
且Sn=Sn﹣1+an﹣1+ ,数列{bn}满足b1=﹣
,数列{bn}满足b1=﹣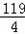
且3bn﹣bn﹣1=n(n≥2且n∈N*).
(1)求{an}的通项公式;
(2)求证:数列{bn﹣an}为等比数列;
(3)求{bn}前n项和的最小值.
(1)由Sn=Sn﹣1+an﹣1+ ,得Sn﹣Sn﹣1=an﹣1+
,得Sn﹣Sn﹣1=an﹣1+ ,2an=2a n﹣1+1,an=a n﹣1+
,2an=2a n﹣1+1,an=a n﹣1+
∴an=a1+(n﹣1)d= n﹣
n﹣
(2)证明:∵3bn﹣bn﹣1=n,∴bn= bn﹣1+
bn﹣1+ n,
n,
∴bn﹣an= bn﹣1+
bn﹣1+ n﹣
n﹣ n+
n+ =
= bn﹣1﹣
bn﹣1﹣ n+
n+ =
= (bn﹣1﹣
(bn﹣1﹣ n+
n+ );
);
bn﹣1﹣an﹣1=bn﹣1﹣ (n﹣1)+
(n﹣1)+ =bn﹣1﹣
=bn﹣1﹣ n+
n+ ;
;
∴由上面两式得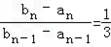 ,
,
又b1﹣a1=﹣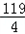 ﹣
﹣ =﹣30
=﹣30
∴数列{bn﹣an}是以﹣30为首项, 为公比的等比数列.
为公比的等比数列.
(3)由(2)得bn﹣an=﹣30×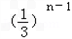 ,
,
∴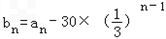 =
=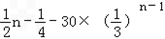 ,
,
bn﹣bn﹣1=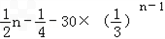
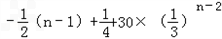
=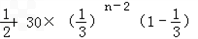 =
=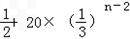 >0,
>0,
∴{bn}是递增数列当n=1时,
b1=﹣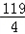 <0;
<0;
当n=2时,b2=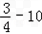 <0;
<0;
当n=3时,b3=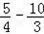 <0;
<0;
当n=4时,b4=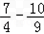 >0,
>0,
所以,从第4项起的各项均大于0,故前3项之和最小.
且S3=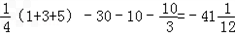 .
.
 ,得Sn﹣Sn﹣1=an﹣1+
,得Sn﹣Sn﹣1=an﹣1+ ,2an=2a n﹣1+1,an=a n﹣1+
,2an=2a n﹣1+1,an=a n﹣1+
∴an=a1+(n﹣1)d=
 n﹣
n﹣
(2)证明:∵3bn﹣bn﹣1=n,∴bn=
 bn﹣1+
bn﹣1+ n,
n,∴bn﹣an=
 bn﹣1+
bn﹣1+ n﹣
n﹣ n+
n+ =
= bn﹣1﹣
bn﹣1﹣ n+
n+ =
= (bn﹣1﹣
(bn﹣1﹣ n+
n+ );
);bn﹣1﹣an﹣1=bn﹣1﹣
 (n﹣1)+
(n﹣1)+ =bn﹣1﹣
=bn﹣1﹣ n+
n+ ;
;∴由上面两式得
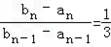 ,
,又b1﹣a1=﹣
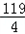 ﹣
﹣ =﹣30
=﹣30∴数列{bn﹣an}是以﹣30为首项,
 为公比的等比数列.
为公比的等比数列.(3)由(2)得bn﹣an=﹣30×
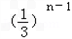 ,
,∴
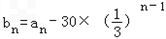 =
=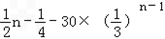 ,
,bn﹣bn﹣1=
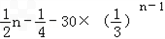
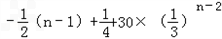
=
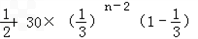 =
=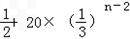 >0,
>0,∴{bn}是递增数列当n=1时,
b1=﹣
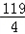 <0;
<0;当n=2时,b2=
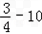 <0;
<0;当n=3时,b3=
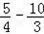 <0;
<0;当n=4时,b4=
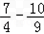 >0,
>0,所以,从第4项起的各项均大于0,故前3项之和最小.
且S3=
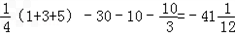 .
.
练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |