题目内容
已知函数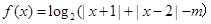 .
.
(1)当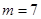 时,求函数
时,求函数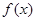 的定义域;
的定义域;
(2)若关于 的不等式
的不等式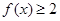 的解集是
的解集是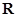 ,求
,求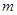 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由题设知: , 1分
, 1分
不等式的解集是以下不等式组解集的并集: ,或
,或 ,或
,或 4分
4分
解得函数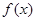 的定义域为
的定义域为 ; 6分
; 6分
(2)不等式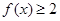 即
即 , 8分
, 8分 时,恒有
时,恒有 , 10分
, 10分
不等式 解集是R,
解集是R, 的取值范围是
的取值范围是 12分
12分
考点:本题主要考查对数函数的性质,简单不等式组的解法,和绝对值不等式恒成立问题,绝对值的几何意义。
点评:中档题,由对数的真数大于0可得到,x的不等式组,进一步求函数的定义域。恒成立问题的解法,往往转化成求函数的最值问题。本题利用绝对值的性质,求得了绝对值之和的最小值,从而进一步建立m的不等式。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系; 表示摩托车厂一天的销售成本与销售量的关系.
表示摩托车厂一天的销售成本与销售量的关系.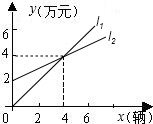
 、纵边
、纵边 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?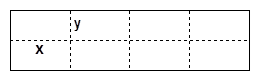
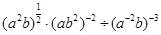 ; (2)计算:
; (2)计算: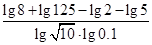 .
. 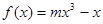 的图象上,以
的图象上,以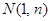 为切点的切线的倾斜角为
为切点的切线的倾斜角为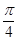 .
.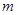 ,
, 的值;
的值;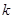 ,使得不等式
,使得不等式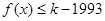 对于
对于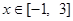 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数 (
(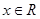 ,
,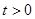 ).
).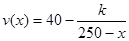 .当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时. 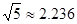 )
)
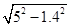 -0.8=4,
-0.8=4, 元/千克,政府补贴为
元/千克,政府补贴为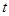 元/千克,根据市场调查,当
元/千克,根据市场调查,当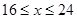 时,这种食品市场日供应量
时,这种食品市场日供应量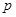 万千克与市场日需量
万千克与市场日需量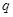 万千克近似地满足关系:
万千克近似地满足关系: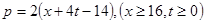 ,
,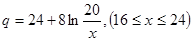 。当
。当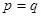 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。