题目内容
（本小题满分12分）已知椭圆长轴端点为
，
为椭圆中心，
为椭圆的右焦点，且
，
（1）求椭圆的标准方程；
（2）记椭圆的上顶点为
，直线
交椭圆于
两点，问：是否存在直线，使点恰好为
的垂心？若存在，求出直线的方程；若不存在，请说明理由。
解：（1）设椭圆方程为
，由题意
，
且
，∴
，椭圆方程为：
………………4分
（2）假设存在直线
，使点
恰好为
的垂心，设
∵
，∴ 故
于是设直线的方程为
………………6分
由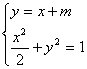
得
即
且
………………8分
又
由
,得
∴
化简得
，解得：
，
………………10分
当时，
三点共线，故舍去
经检验符合条件
故存在直线满足条件，其方程为
………………12分
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
