题目内容
2.设A、B是双曲线x2-$\frac{{y}^{2}}{2}$=λ(λ≠0)上两点,N(1,2)是线段AB的中点,线段AB的垂直平分线交双曲线于C、D两点.(1)确定实数λ的取值范围;(2)试判断A、B、C、D四点是否共圆?说明理由.
分析 (1)设直线AB的方程为yy=k(x-1)+2,代入x2-$\frac{{y}^{2}}{2}$=λ,整理得:(2-k2)x2-2k(2-k)x-(2-k)2-2λ=0,然后结合题设条件确定实数λ的取值范围;
(2)由题设条件可知λ>1,直线CD的方程为y=-x+3,代入双曲线方程,整理得x2+6x-9-2λ=0.将直线AB的方程y=x+1代入双曲线方程整理得x2-2x-1-2λ=0,由此通过计算知$\overrightarrow{CA}•\overrightarrow{DA}$=0,A在以CD为直径的圆上.又B为A关于CD的对称点,可得A、B、C、D四点共圆.
解答 解:(1)依题意,可设直线AB的方程为y=k(x-1)+2,
代入x2-$\frac{{y}^{2}}{2}$=λ,整理得:(2-k2)x2-2k(2-k)x-(2-k)2-2λ=0①
设A(x1,y1),B(x2,y2),则x1,x2是方程①的两个不同的根,
∴△=4k2(2-k)2-4(2-k2)[-(2-k)2-2λ]>0,②
且x1+x2=$\frac{2k(2-k)}{2-{k}^{2}}$.由N(1,2)是线段AB的中点,得x1+x2=2,
∴$\frac{2k(2-k)}{2-{k}^{2}}$=2解得k=1,代入②得λ>1,
即λ的取值范围是(1,+∞).
(2)由(1)知λ>1,
∵CD垂直平分AB,
∴直线CD的方程为y=-x+3,代入双曲线方程,整理得x2+6x-9-2λ=0.③
将直线AB的方程y=x+1代入双曲线方程整理得x2-2x-1-2λ=0.④
解③和④式可得x1,2=-3±$\sqrt{18+2λ}$,x3,4=1±$\sqrt{2+2λ}$,
不妨设A(-3+$\sqrt{18+2λ}$,-2±$\sqrt{18+2λ}$),
C(1+$\sqrt{2+2λ}$,2-$\sqrt{2+2λ}$),D(1-$\sqrt{2+2λ}$,4+$\sqrt{2+2λ}$).
∴可得$\overrightarrow{CA}•\overrightarrow{DA}$=0,
∴A在以CD为直径的圆上.
又B为A关于CD的对称点,
∴A、B、C、D四点共圆.
点评 本题综合考查直线和双曲线的位置关系,难度较大,解题时要仔细审题,注意公式的灵活运用.

| A. | {x|x<3} | B. | {x|x≤3} | C. | {x|-1<x≤3} | D. | {x|-1≤x≤3} |
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$或$\frac{3}{2}$ | D. | 1 |
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\frac{\sqrt{3}}{2}$ |
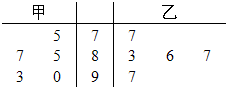 甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示.
甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示.