题目内容
21. 已知常数a>0,在矩形ABCD中,AB=4,BC=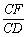
21.解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.按题意有A(-2,0),B(2,0),C(2,
设![]() =
=![]() =
=![]() =k(0≤k≤1).
=k(0≤k≤1).
由此有E(2,4ak),F(2-4k,
直线OF的方程为:2ax+(2k-1)y=0, ①
直线GE的方程为:-a(2k-1)x+y-
从①,②消去参数k,得点P(x,y)坐标满足方程
整理得 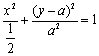 .
.
当a2=![]() 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当a2≠![]() 时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
当a2<![]() 时,点P到椭圆两个焦点(-
时,点P到椭圆两个焦点(-![]() ),(
),(![]() )的距离之和为定值
)的距离之和为定值![]() .
.
当a2>![]() 时,点P到椭圆两个焦点(0,a-
时,点P到椭圆两个焦点(0,a-![]() ),(0,a+
),(0,a+![]() )的距离之和为定值2a.
)的距离之和为定值2a.

练习册系列答案
相关题目
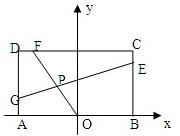 已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且