题目内容
平面上有四个点,设任三点均不共线.求证:以每三个点为顶点的三角形不可能都是锐角三角形.
证明:假设以每三个点为顶点的三角形都是锐角三角形,记四个点为A、B、C、D,考虑点D在△ABC之内与之外这两种情况.
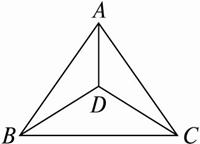
(1)如果点D在△ABC之内,如下图,由假设知围绕点D的三个角都是锐角,其和小于270°,这与一个周角等于360°相矛盾.
(2)如果点D在△ABC之外,如下图,由假设知∠A、∠B、∠C、∠D都小于90°,这与四边形的内角和为360°相矛盾.
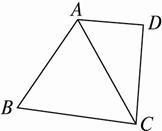
综上所述,假设不成立,从而题目中的结论成立.

练习册系列答案
相关题目