题目内容
已知函数f(x)=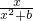 ,其中b∈R.
,其中b∈R.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设b>0.若?x∈[ ,
, ],使f(x)≥1,求b的取值范围.
],使f(x)≥1,求b的取值范围.
解:(Ⅰ)①当b=0时,f(x)= .
.
故f(x)的单调减区间为(-∞,0),(0,+∞);无单调增区间.
②当b>0时,f′(x)=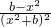 .
.
令f′(x)=0,得x1= ,x2=-
,x2=- .
.
f(x)和f′(x)的情况如下:
故f(x)的单调减区间为(-∞,- ),(
),( ,+∞);单调增区间为(-
,+∞);单调增区间为(- ,
, ).
).
③当b<0时,f(x)的定义域为D={x∈R|x≠± }.
}.
因为f′(x)=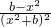 <0在D上恒成立,
<0在D上恒成立,
故f(x)的单调减区间为(-∞,- ),(-
),(- ,
, ),(
),( ,+∞);无单调增区间.
,+∞);无单调增区间.
(Ⅱ)解:因为b>0,x∈[ ,
, ],
],
所以f(x)≥1等价于b≤-x2+x,其中x∈[ ,
, ].
].
设g(x)=-x2+x,g(x)在区间[ ,
, ]上的最大值为g(
]上的最大值为g( )=
)= .
.
则“?x∈[ ,
, ],使得b≤-x2+x”等价于b≤
],使得b≤-x2+x”等价于b≤ .
.
所以b的取值范围是(0, ].
].
分析:(Ⅰ)分情况讨论:①当b=0时,②当b>0时,③当b<0时,然后利用导数即可求得单调区间;
(Ⅱ)f(x)≥1等价于b≤-x2+x,g(x)=-x2+x,则“?x∈[ ,
, ],使得b≤-x2+x”等价于b小于等于g(x)在区间[
],使得b≤-x2+x”等价于b小于等于g(x)在区间[ ,
, ]上的最大值.
]上的最大值.
点评:本题考查利用导数研究函数的单调性、函数恒成立及函数在区间上的最值问题,考查学生综合运用所学知识分析问题解决问题的能力.
 .
.故f(x)的单调减区间为(-∞,0),(0,+∞);无单调增区间.
②当b>0时,f′(x)=
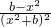 .
. 令f′(x)=0,得x1=
 ,x2=-
,x2=- .
.f(x)和f′(x)的情况如下:
| x | (-∞,- ) ) | - | (- , , ) ) |  | ( ,+∞) ,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | ↗ | ↘ |
 ),(
),( ,+∞);单调增区间为(-
,+∞);单调增区间为(- ,
, ).
).③当b<0时,f(x)的定义域为D={x∈R|x≠±
 }.
}.因为f′(x)=
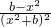 <0在D上恒成立,
<0在D上恒成立,故f(x)的单调减区间为(-∞,-
 ),(-
),(- ,
, ),(
),( ,+∞);无单调增区间.
,+∞);无单调增区间.(Ⅱ)解:因为b>0,x∈[
 ,
, ],
],所以f(x)≥1等价于b≤-x2+x,其中x∈[
 ,
, ].
].设g(x)=-x2+x,g(x)在区间[
 ,
, ]上的最大值为g(
]上的最大值为g( )=
)= .
.则“?x∈[
 ,
, ],使得b≤-x2+x”等价于b≤
],使得b≤-x2+x”等价于b≤ .
.所以b的取值范围是(0,
 ].
].分析:(Ⅰ)分情况讨论:①当b=0时,②当b>0时,③当b<0时,然后利用导数即可求得单调区间;
(Ⅱ)f(x)≥1等价于b≤-x2+x,g(x)=-x2+x,则“?x∈[
 ,
, ],使得b≤-x2+x”等价于b小于等于g(x)在区间[
],使得b≤-x2+x”等价于b小于等于g(x)在区间[ ,
, ]上的最大值.
]上的最大值.点评:本题考查利用导数研究函数的单调性、函数恒成立及函数在区间上的最值问题,考查学生综合运用所学知识分析问题解决问题的能力.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|