题目内容

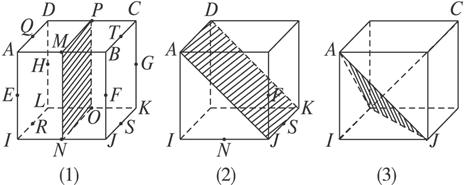
如图2-3-20,在正方体ABCD—A1B1C1D1中,E、F分别为BB1、CD的中点.

求证:平面AED⊥平面A1FD1.

图2-3-20

思路分析:构造出平面AED、平面A1FD1与正方体的截面及交线.:取C1C中点N,连结EN、DN,则EN∥AD,

图2-3-21

∴平面AED即平面AEND.

取AB中点M,连结FM、A1M,则D1F∥A1M,

∴平面A1FD1即平面A1MFD1.

设A1M∩AE=O,FD1∩DN=O1,则OO1为平面AED与平面A1FD1的交线,OO1∥AD且AE⊥A1M.

∵AD⊥平面ABB1A1,

∴OO1⊥平面ABB1A1.

∵AO、OE平面ABB1A1,

∴OO1⊥AO,OO1⊥OE,

从而∠A1OE为平面AED与平面A1FD1所成的二面角的平面角.

由AE⊥A1M,知∠A1OE=90°.

故平面AED⊥平面A1FD1.


练习册系列答案
相关题目
（1）如图1，这段伪代码的功能是
统计x1到x10十个数据中负数的个数
统计x1到x10十个数据中负数的个数
．
（2）如图2，下列算法输出的结果是（写式子）
5+
1
32
+
1
33
+…+ 
1
312
5+
1
32
+
1
33
+…+ 
1
312
．
（3）如图为一个求20个数的平均数的程序，在横线上应填充的语句为
i＞20
i＞20
．
“世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识，为此某网站进行了持续一周的在线调查，共有200人参加调查，现将数据整理分组如题中表格所示．
序号（i） 分组睡眠时间 组中值（mi） 频数
（人数）		 频率
（fi）
1 [4，5） 4.5 8 0.04
2 [5，6） 5.5 52 0.26
3 [6，7） 6.5 60 0.30
4 [7，8） 7.5 56 0.28
5 [8，9） 8.5 20 0.10
6 [9，10] 9.5 4 0.02

（1）在答题卡给定的坐标系中画出频率分布直方图；
（2）睡眠时间小于8的概率是多少？
（3）为了对数据进行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图（如图2），求输出的S的值，并说明S的统计意义．
一张矩形纸片，剪下一个正方形，剩下一个矩形，称为第一次操作；在剩下的矩形纸片中再剪下一个正方形，剩下一个矩形，称为第二次操作；…；若在第n次操作后，剩下的矩形为正方形，则称原矩形为n阶奇异矩形．如图1，矩形ABCD中，若AB=2，BC=6，则称矩形ABCD为2阶奇异矩形．
（1）判断与操作：
如图2，矩形ABCD长为5，宽为2，它是奇异矩形吗？如果是，请写出它是几阶奇异矩形，并在图中画出裁剪线；如果不是，请说明理由．
（2）探究与计算：
已知矩形ABCD的一边长为20，另一边长为a（a＜20），且它是3阶奇异矩形，请画出矩形ABCD及裁剪线的示意图，并在图的下方写出a的值．
（3）归纳与拓展：
已知矩形ABCD两邻边的长分别为b，c（b＜c），且它是4阶奇异矩形，求b：c（直接写出结果）．精英家教网
如图2-3-9,正方体有8个顶点和12条棱,每条棱上均有一个中点,于是有棱的中点12个,顶点与中点合起来共有20个〔图2-3-9(1)〕.过其中的两点可作一条直线;过其中不在同一直线上的三点可作一个平面.现在考虑这些直线与平面的垂直关系.

                                      图2-3-9

(1)试举出一直线与一平面相互垂直的例子(不少于4例).

(2)若一直线与一平面相互垂直,我们就说这条直线与这个平面构成了一个“垂直关系组”,两个“垂直关系组”当且仅当其中两条直线和两个平面不全同一时称为相异的(或不同的).试求与正方体的棱相关的“垂直关系组”的个数.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网