题目内容
(文科)(13分)在如图所示的空间几何体中,△ABC,△ACD都是等边三角形,AE=CE,DE//平面ABC,平面ACD⊥平面ABC.
(1)求证:DE⊥平面ACD;(2)若AB=BE=2,求多面体ABCDE的体积.
(文科)
解:(1)法一:△ABC,△ACD都是等边三角形,
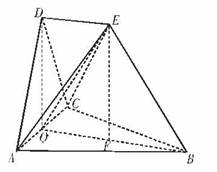 AE=CE,取AC中点O,连接BO,DO,EO,则
AE=CE,取AC中点O,连接BO,DO,EO,则
BO⊥AC,DO⊥AC,EO⊥AC ……………2分

![]() ,
,
![]()
![]() ODEF是平面四边形 ………………4分
ODEF是平面四边形 ………………4分
![]()
![]() 平面ACD ………………6分
平面ACD ………………6分
法二:△ABC,△ACD都是等边三角形,
AE=CE,取AC中点O,连接BO,DO,EO,则
BO⊥AC,DO⊥AC,EO⊥AC ……………2分
![]() ,
,![]() 平面OBE
平面OBE
![]() 即OB,OD,OE
即OB,OD,OE![]() 平面OBED
平面OBED
又![]() 平面ABC,
平面ABC,![]() DE//BO ………………4分
DE//BO ………………4分
![]()
∴DE⊥平面ACD ………………6分
(2)由EF//DO,DE//OF,知DE=OF,EF=DO,
又AB=BE=2,△ABC,△ACD都是等边三角形,EF⊥BO
![]() ………………8分
………………8分
![]() 平面ACD,
平面ACD,
![]() ;
;
又三棱锥E—ABC的体积![]() ………………12分
………………12分
∴多面体ABCDE的体积为![]() ………………13分
………………13分

练习册系列答案
相关题目
 某校高三文科分为五个班.高三数学测试后,随机地在各班抽取部分学生进行成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了18人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
某校高三文科分为五个班.高三数学测试后,随机地在各班抽取部分学生进行成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了18人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.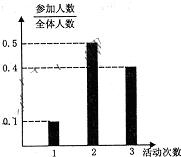 (理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示. 某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人. 某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.