题目内容
已知抛物线y2=4x的准线与双曲线
-y2=1 (a>0)交于A,B两点,点F为抛物线的焦点,若△FAB为直角三角形,则a的值为( )
| x2 |
| a2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:求出抛物线的准线为x=-1,焦点为F(1,0).根据对称性可得△FAB是等腰直角三角形,从而算出A、B的坐标,将其代入双曲线方程,解关于a的等式即可得到实数a的值.
解答:解: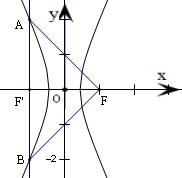 ∵抛物线的方程为y2=4x,
∵抛物线的方程为y2=4x,
∴抛物线的准线为x=-1,焦点为F(1,0).
又∵直线x=-1交双曲线
-y2=1于A、B两点,△FAB为直角三角形.
∴△FAB是等腰直角三角形,AB边上的高FF'=2
由此可得A(-1,2)、B(-1,-2),如图所示
将点A或点B的坐标代入双曲线方程,得
-4=1,解之得a=
(舍负)
故选:D
 ∵抛物线的方程为y2=4x,
∵抛物线的方程为y2=4x,∴抛物线的准线为x=-1,焦点为F(1,0).
又∵直线x=-1交双曲线
| x2 |
| a2 |
∴△FAB是等腰直角三角形,AB边上的高FF'=2
由此可得A(-1,2)、B(-1,-2),如图所示
将点A或点B的坐标代入双曲线方程,得
| 1 |
| a2 |
| ||
| 5 |
故选:D
点评:本题给出抛物线与双曲线满足的条件,在已知抛物线的方程情况下求双曲线的标准方程.着重考查了抛物线、双曲线的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.
已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.